T
Teach Me AnythingTMA
Video History
Page 7 / 126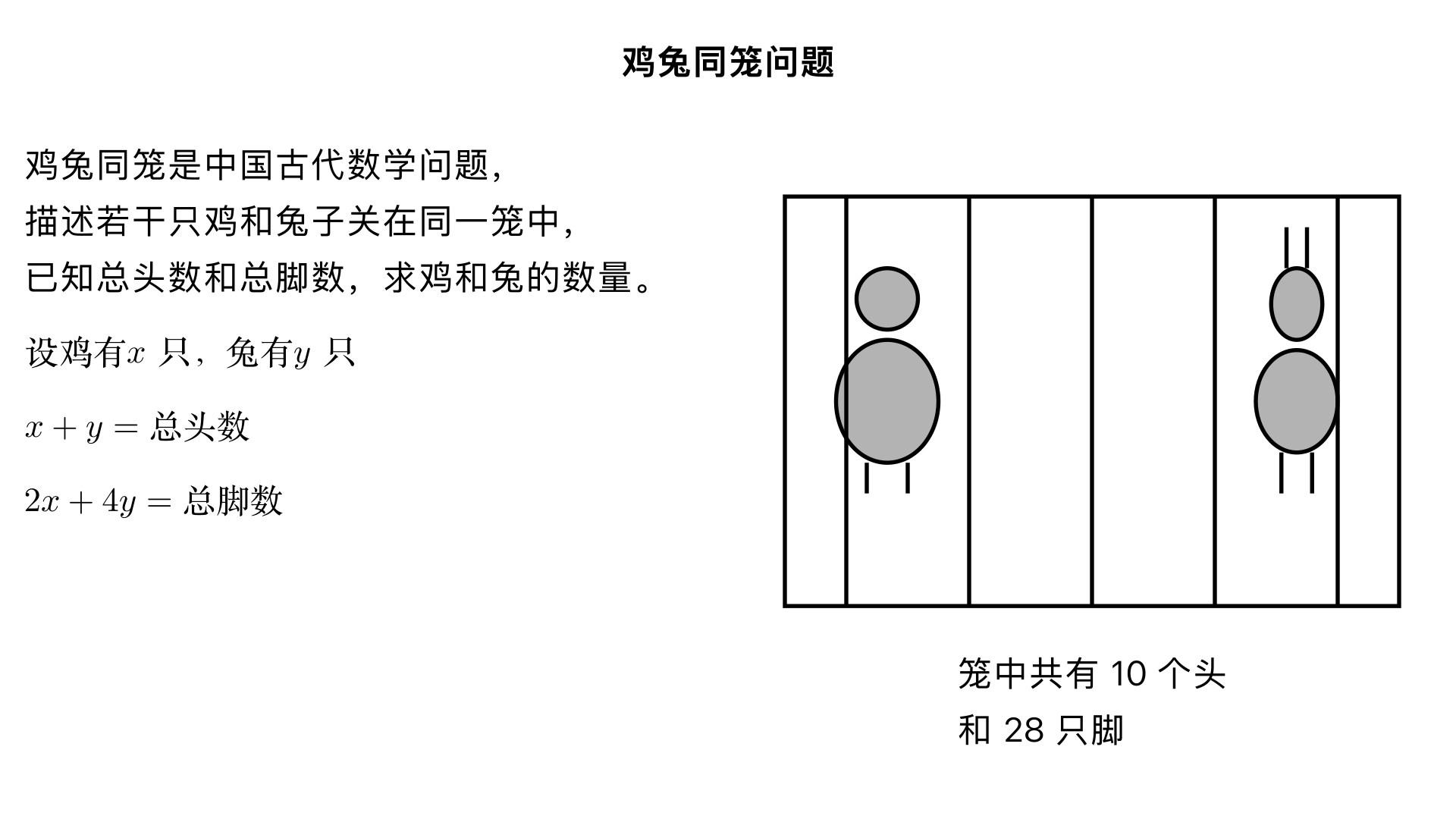
▶
鸡兔同笼的问题
▶
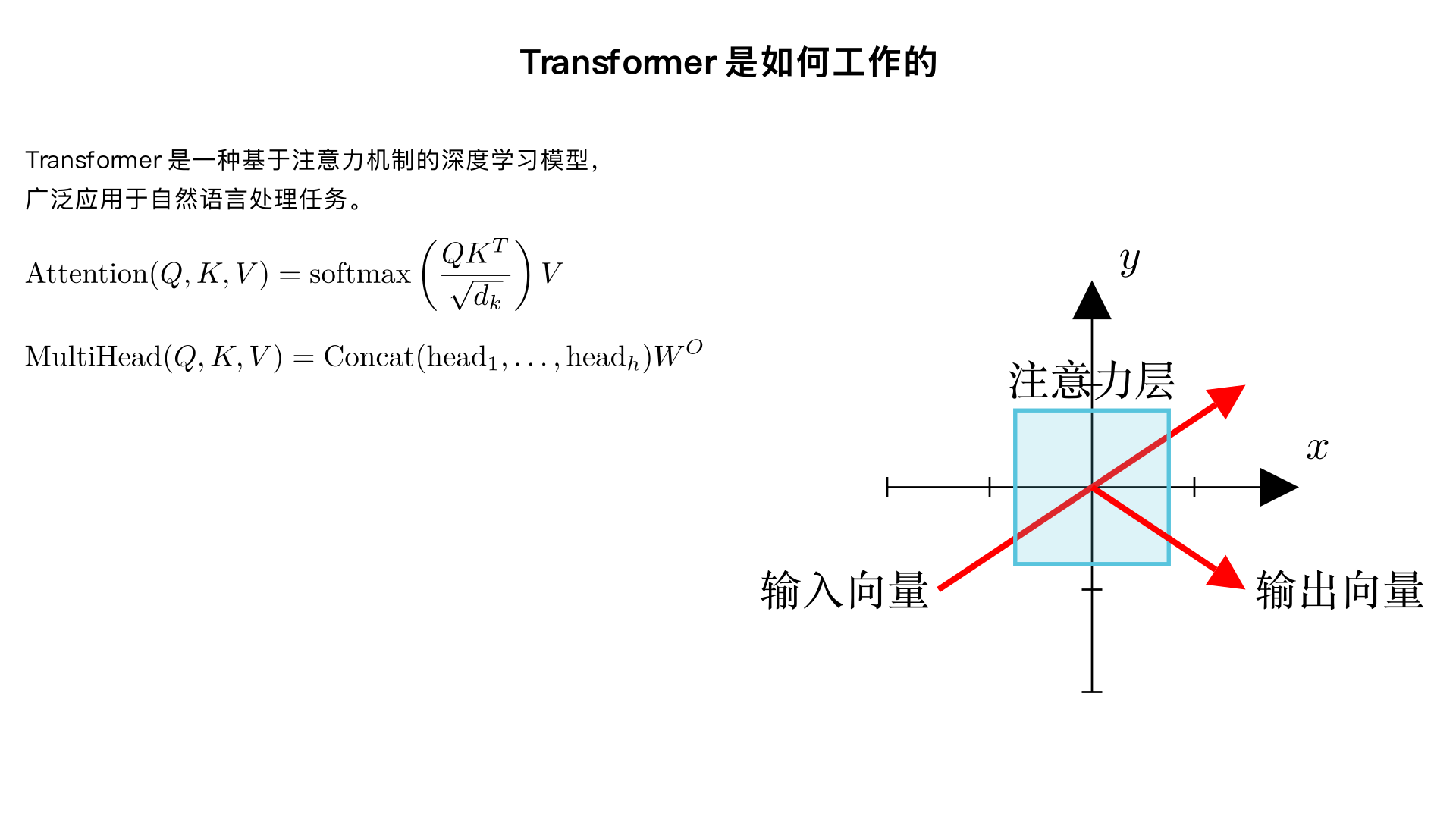
transformer是如何工作的

▶
In the heart of the African savanna, a group of researchers stumbled upon a rare sight—a baby rhinoceros struggling in a poacher's trap. With careful precision, they freed the frightened calf, who they named Luna. Despite her initial fear, Luna quickly bonded with the team, finding solace and safety in their care. Over time, Luna grew stronger and more confident, her playful spirit bringing joy to all around her. As she matured, Luna became a symbol of resilience and hope, a beacon of light in a world often filled with darkness. With the researchers' guidance, Luna eventually returned to the wild, her indomitable spirit a reminder of the power of compassion and perseverance.
▶
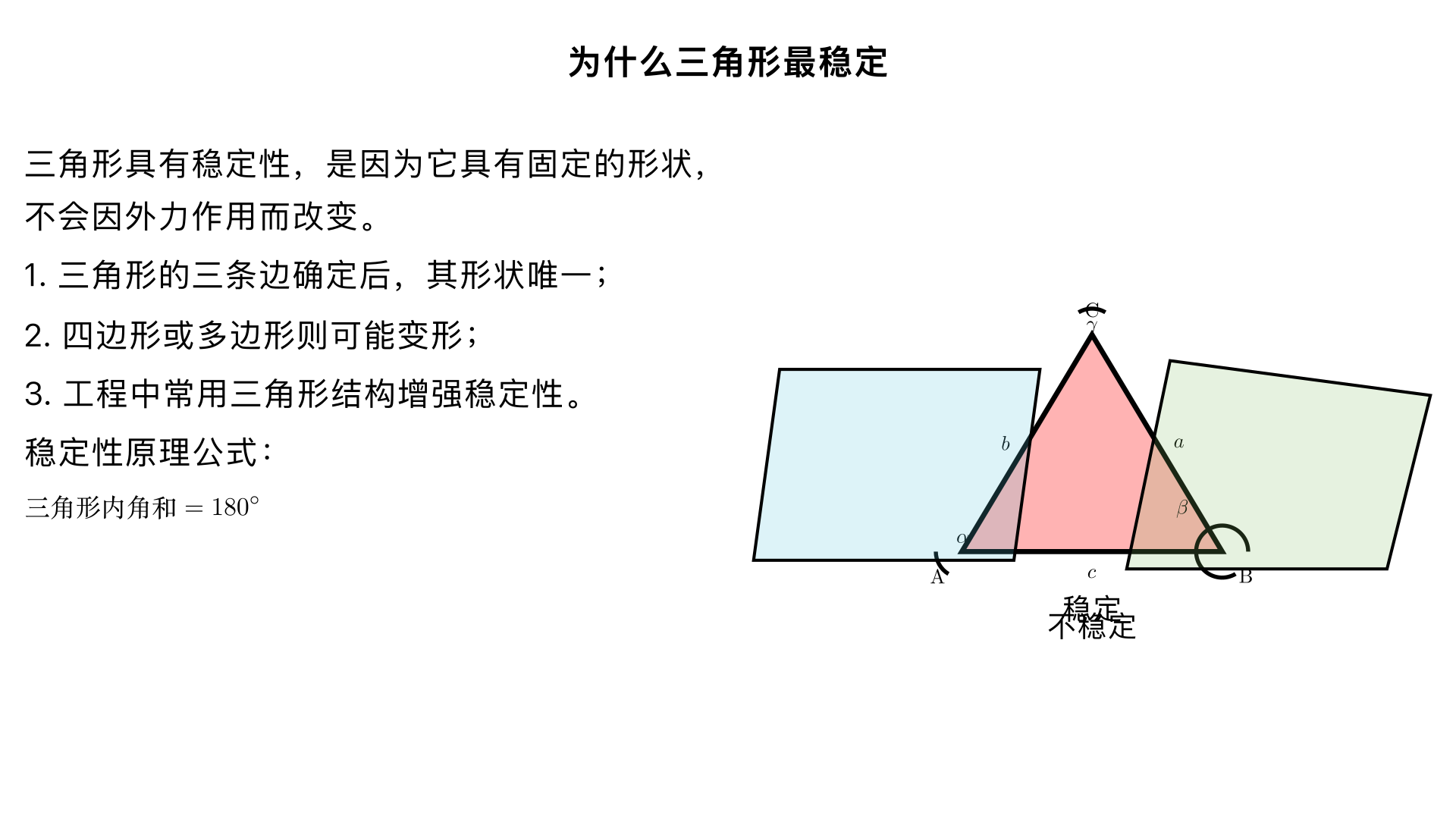
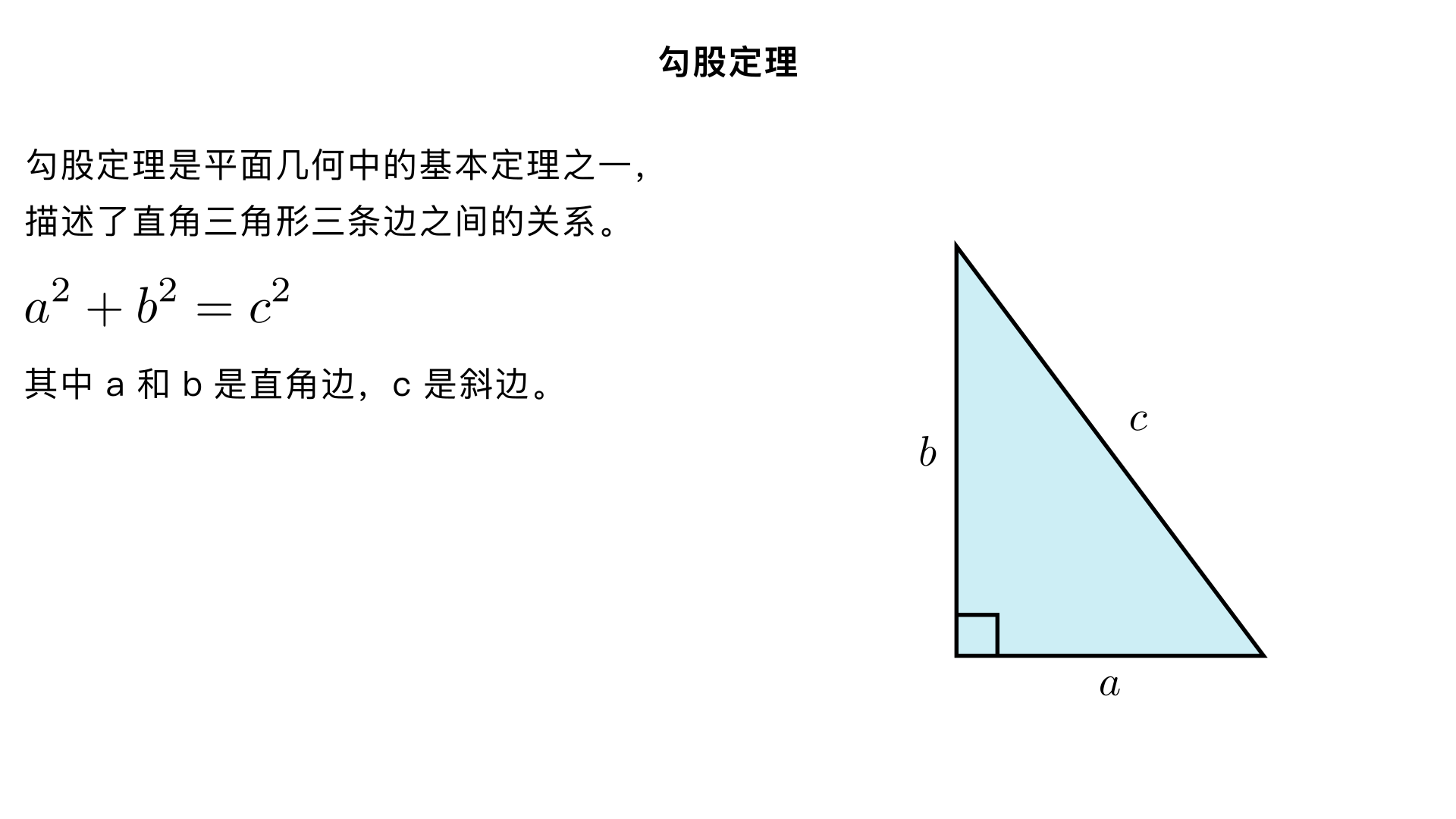
为什么三角形最稳定
▶
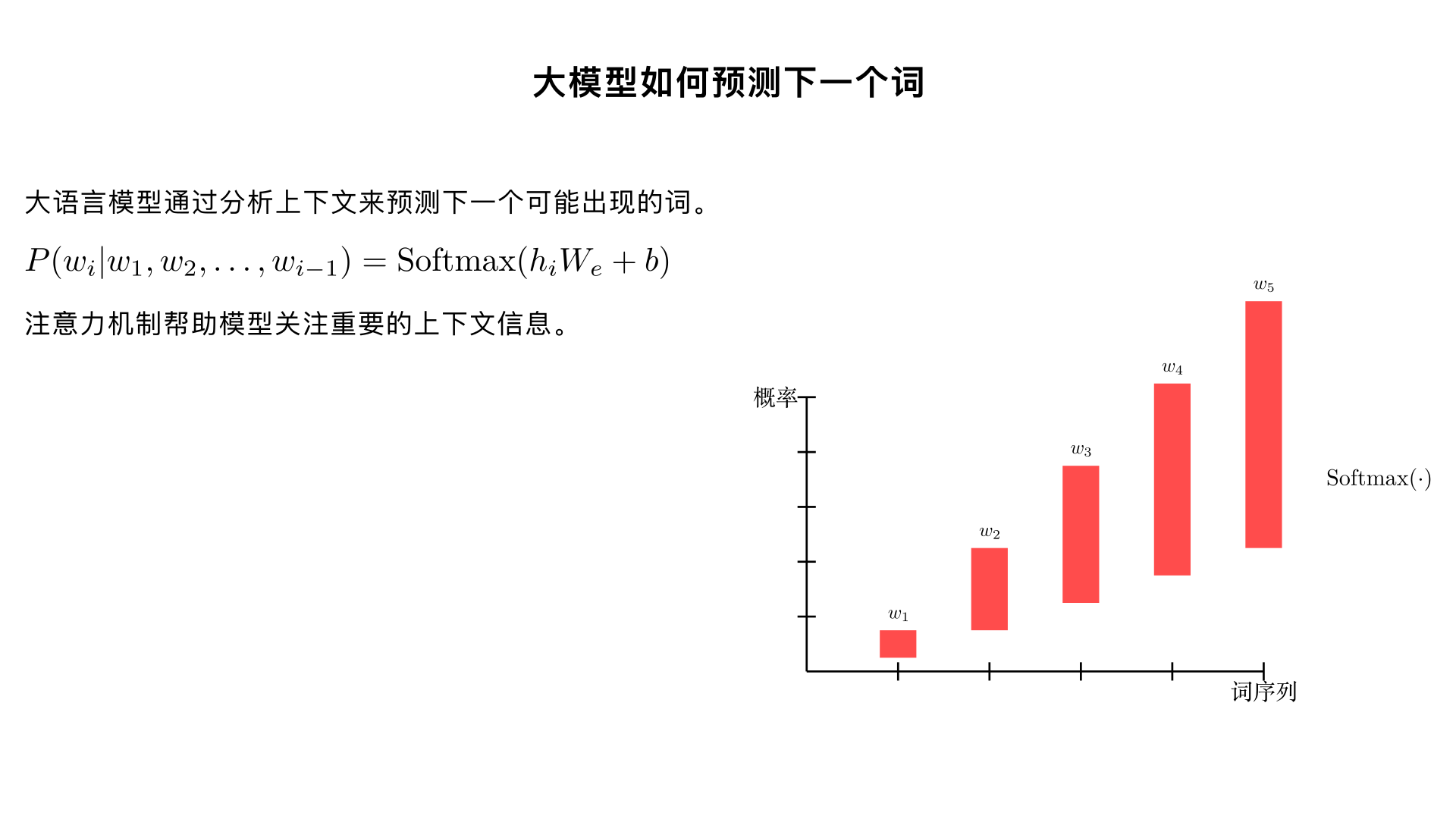
大模型如何预测下一个词
▶
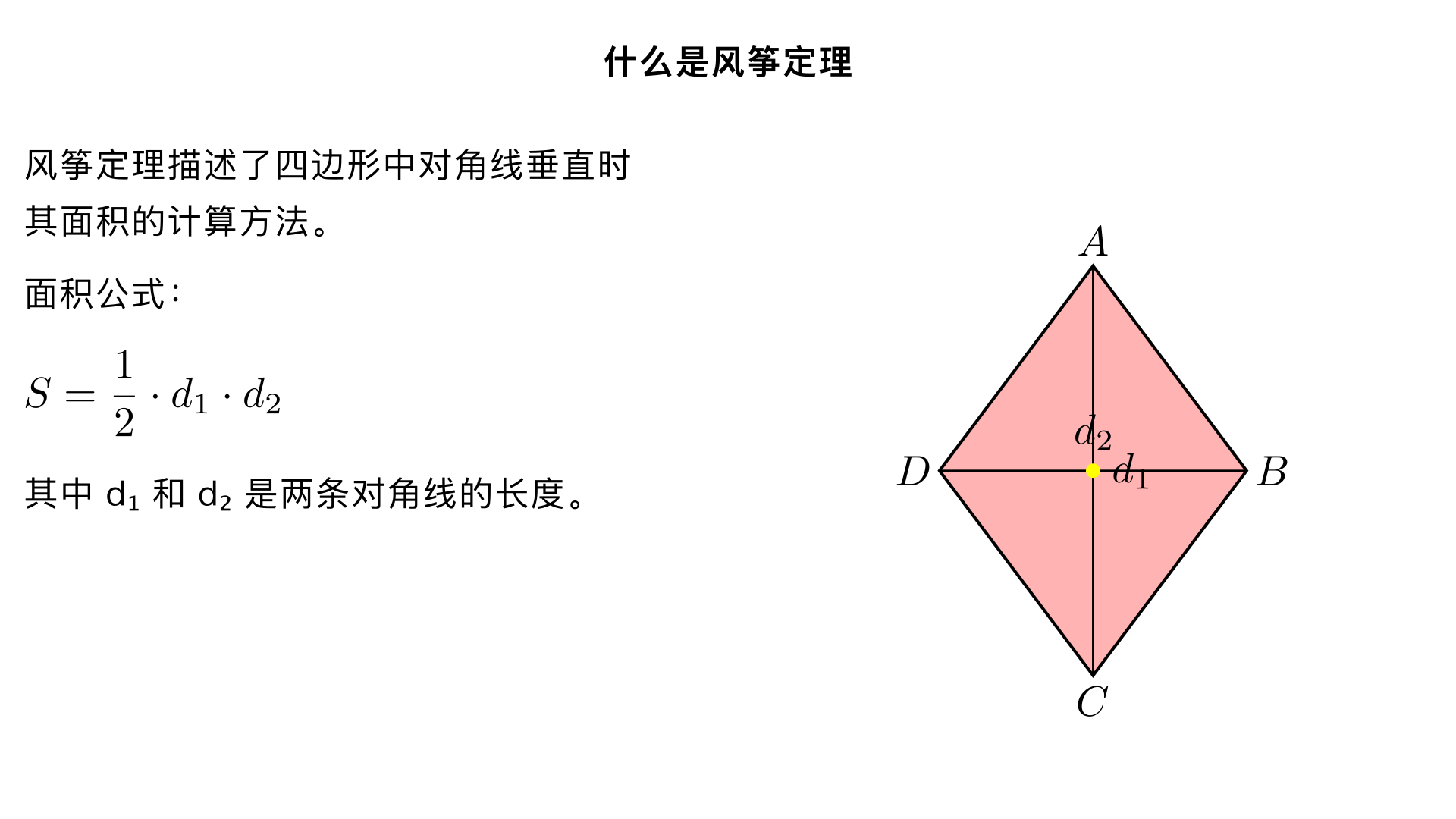
什么是风筝定理
▶
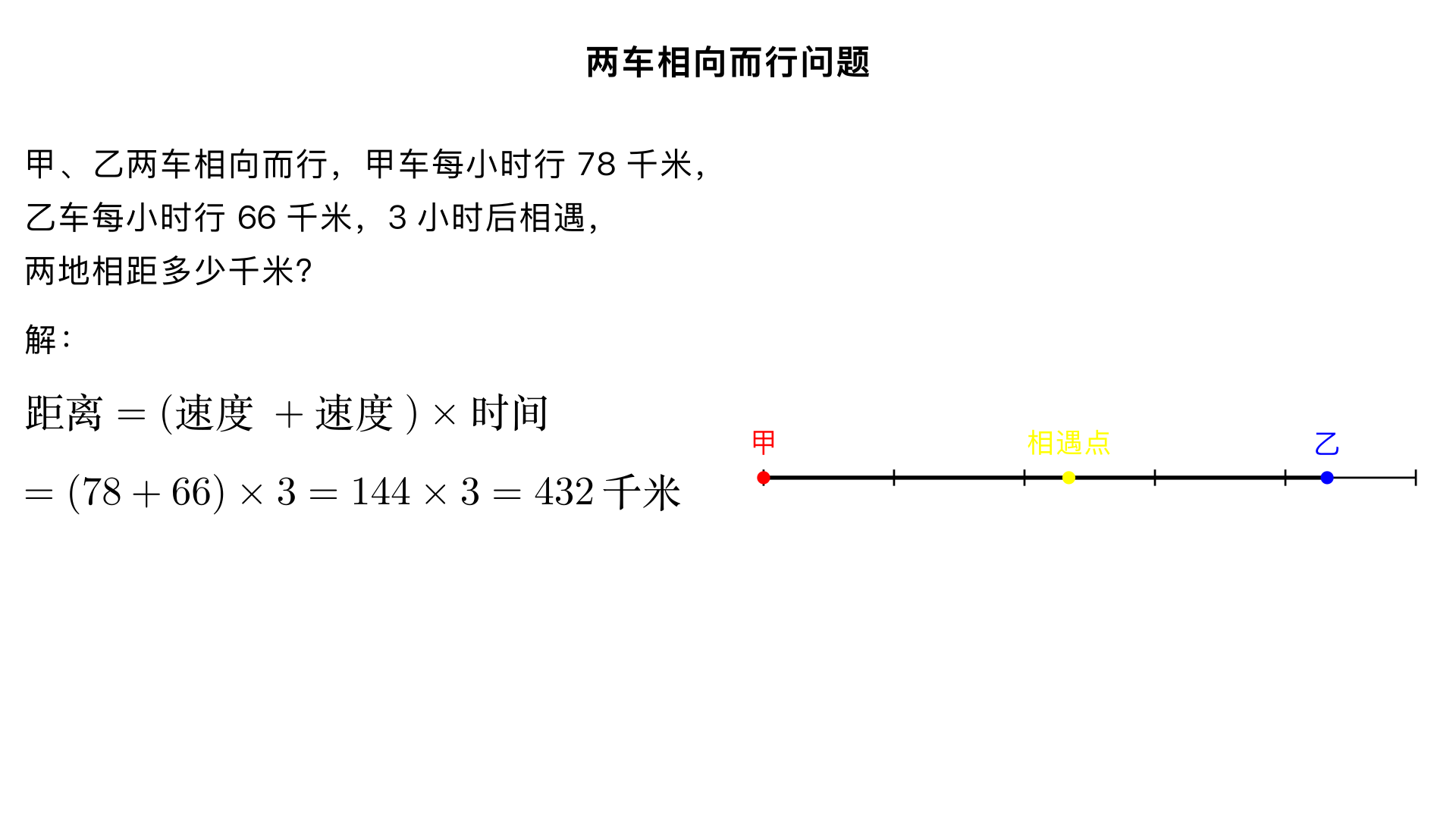
甲、乙两车相向而行,甲车每小时行 78 千米,乙车每小时行 66 千米,3 小时后相遇,两地相距多少千米?
▶
怎么系统学习英语口语
▶
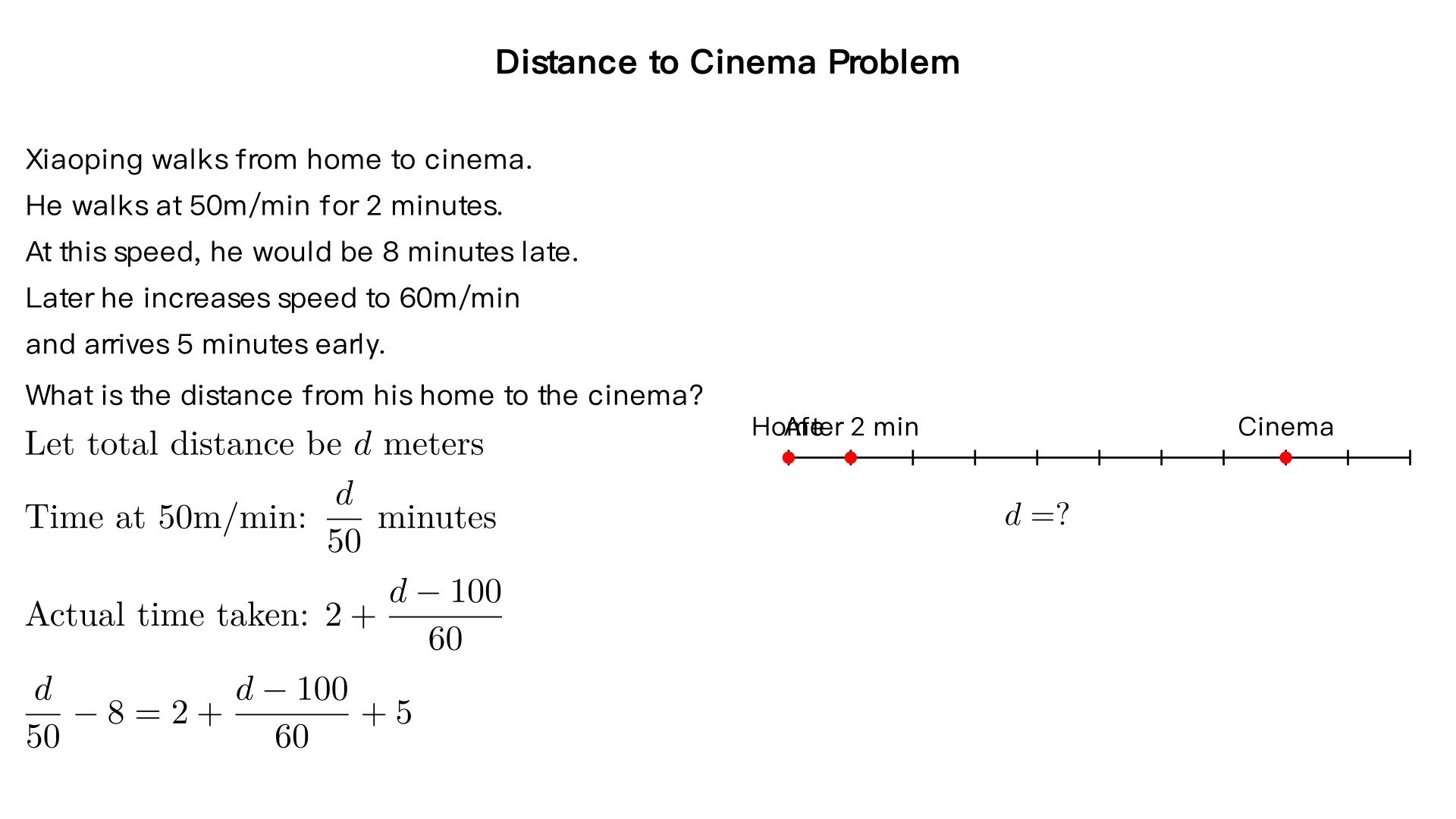
小平从家到电影院去看电影,先用每分钟50米的速度走了2分钟,如果这样走下去,他看电影就要迟到8分钟,后来他改用每分钟60米的速度前进,结果提前5分钟到达电影院,小平的家到电影院的距离是多少米

▶
小平从家到电影院去看电影,先用每分钟50米的速度走了2分钟,如果这样走下去,他看电影就要迟到8分钟,后来他改用每分钟60米的速度前进,结果提前5分钟到达电影院,小平的家到电影院的距离是多少米
▶
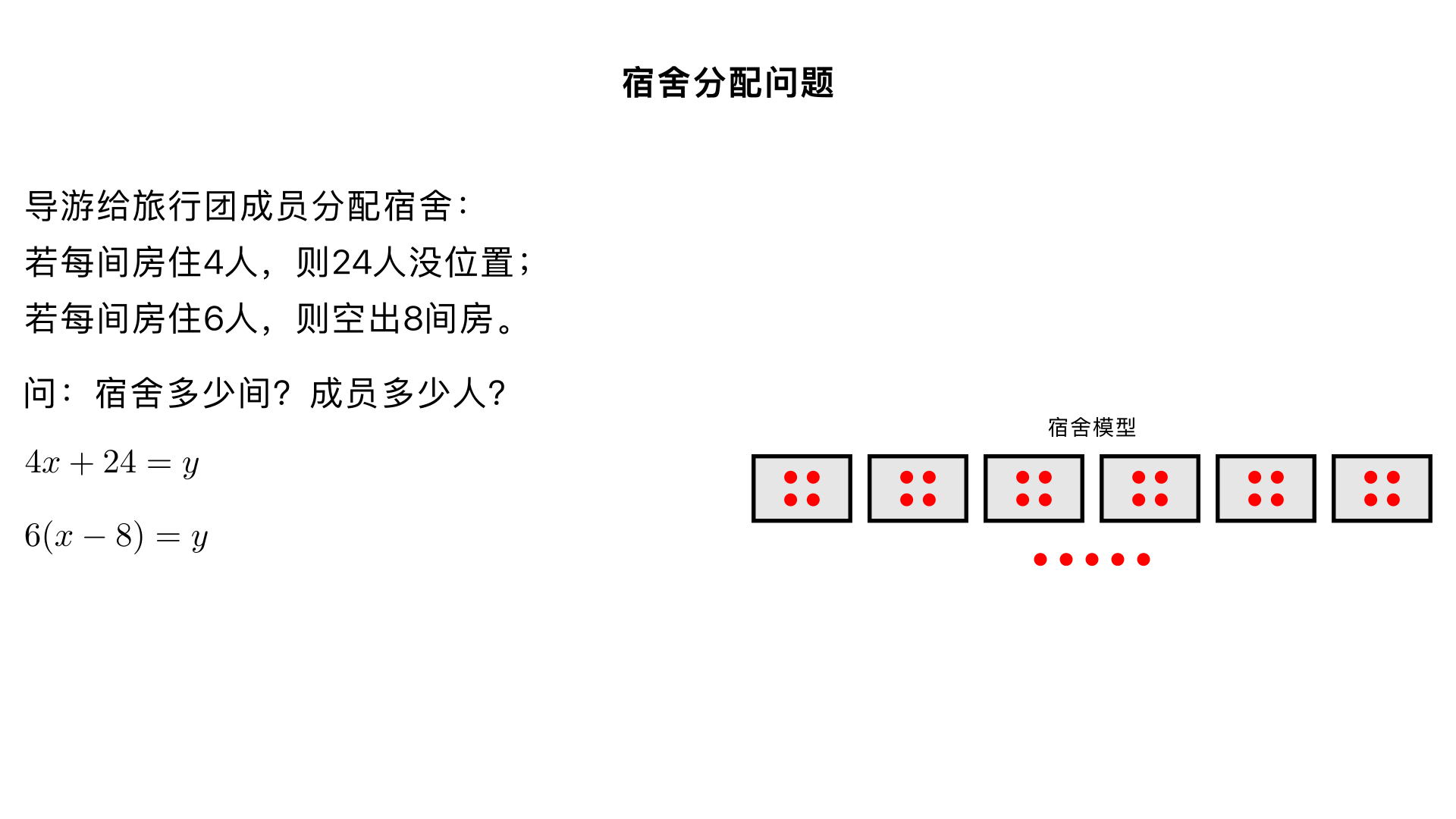
导游给某旅行团的成员分配宿会,如果每个房间住4人,则24人没有位置.如果每个房间住6人,则空出8个房间,求宿舍有多少间旅行团的成员有多少人?
▶