T
Teach Me AnythingTMA
Video History
Page 8 / 126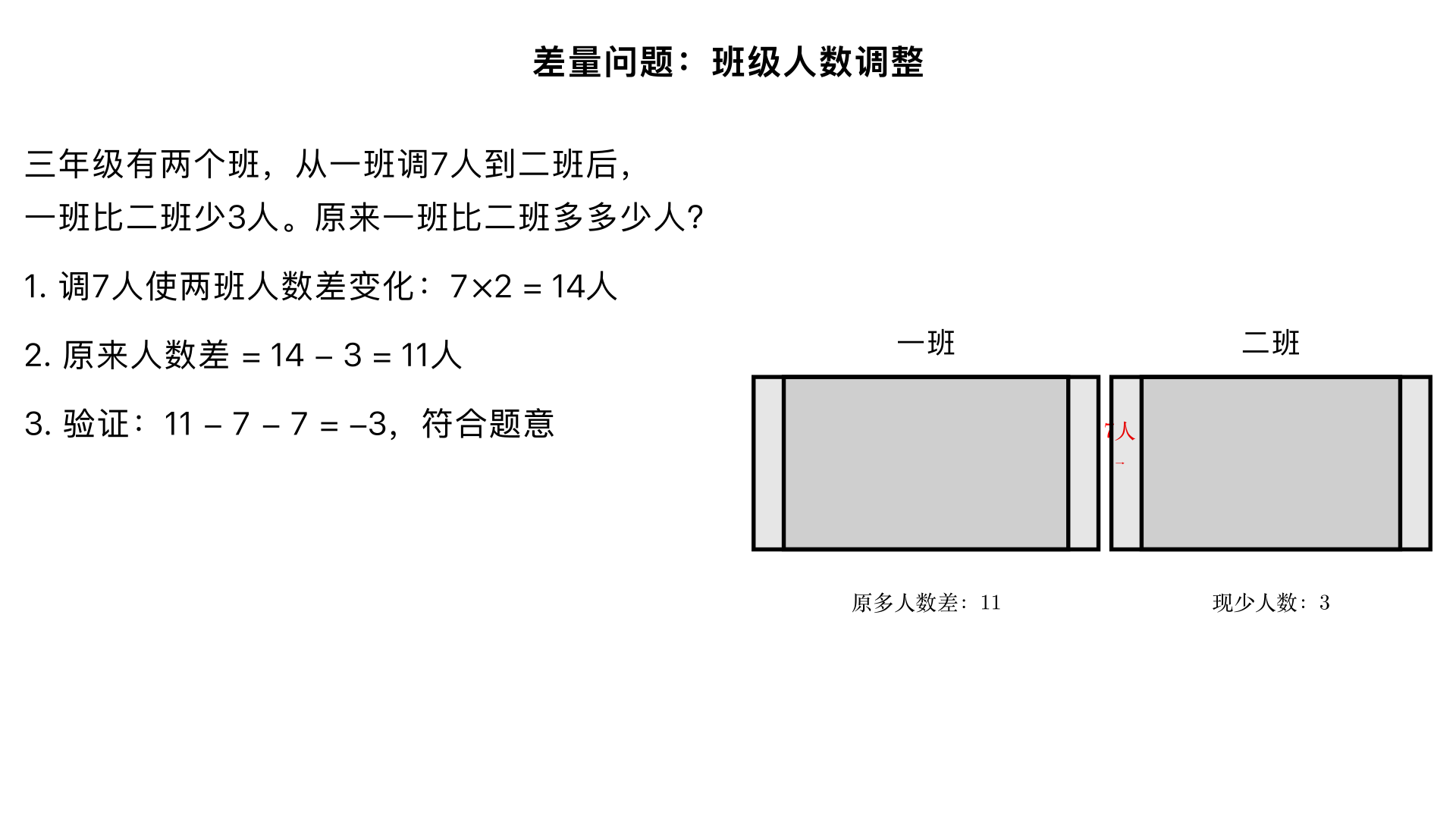
▶
差量问题:三年级有两个班,如果从一班调7人到二班去,一班就比二班少3人。原来一班比二班多多少人? 一、题型判断:差量问题(小学奥数 “移多补少” 子类) 这类题型的核心是理解 “移动人数” 与 “两班人数差” 的关系,解题关键是抓住 “移动后人数差”,反向推算原来的人数差,本质是 “数量移动过程中,总差量的变化规律” 应用,是三年级奥数高频基础题型。 二、解题过程(分 3 步:分析移动后的差量→推导原来的差量→得出结果) 已知条件: 操作:从一班调 7 人到二班; 结果:移动后,一班比二班少 3 人;核心逻辑:调人时,一班减少 7 人、二班增加 7 人,单方向移动 1 人,两班人数差会减少 2 人(一班少 1,二班多 1,差距少 2),先算移动导致的差量变化,再结合移动后的差量,推出原来的差量。 步骤 1:计算 “调 7 人” 导致的两班人数差变化 从一班调 7 人到二班,相当于: 一班人数:-7 人; 二班人数:+7 人; 两班人数差的变化量:7×2 = 14 人(即原来的人数差,比移动后的人数差多 14 人);(通俗理解:本来一班比二班多一些人,调走 7 人后,一班少了、二班多了,差距一下子缩小了 14 人) 步骤 2:结合移动后的差量,推导原来的人数差 移动后,一班比二班少 3 人(即:二班比一班多 3 人);原来的人数差 = 移动导致的差量变化 - 移动后的反向差量;列式:14 - 3 = 11 人;(核心逻辑:原来一班比二班多的人数,减去缩小的 14 人后,反而比二班少 3 人,因此原来的差是 14-3=11) 步骤 3:验证逻辑(简化理解,辅助计算) 假设原来一班比二班多 11 人,按操作调 7 人: 一班减少 7 人,二班增加 7 人,此时一班比二班多:11 - 7 - 7 = -3 人; 即一班比二班少 3 人,与题目条件完全匹配,计算正确。 三、反推验证(逐一对接条件,确认无误差) 假设原来一班比二班多 11 人,设二班原有 x 人,一班原有 x+11 人; 调 7 人后:一班人数 = x+11-7=x+4,二班人数 = x+7; 移动后人数差:二班 - 一班 = (x+7) - (x+4) = 3 人,与题目 “一班比二班少 3 人” 一致 ✔️; 差量变化验证:调 7 人,差量缩小 7×2=14 人,11-14=-3,完全符合逻辑 ✔️; 反向验证:若原来一班比二班多 11 人,调 7 人后差 3 人,无计算误差,逻辑闭环 ✔️。 四、最终结果 原来一班比二班多 11 人。
▶
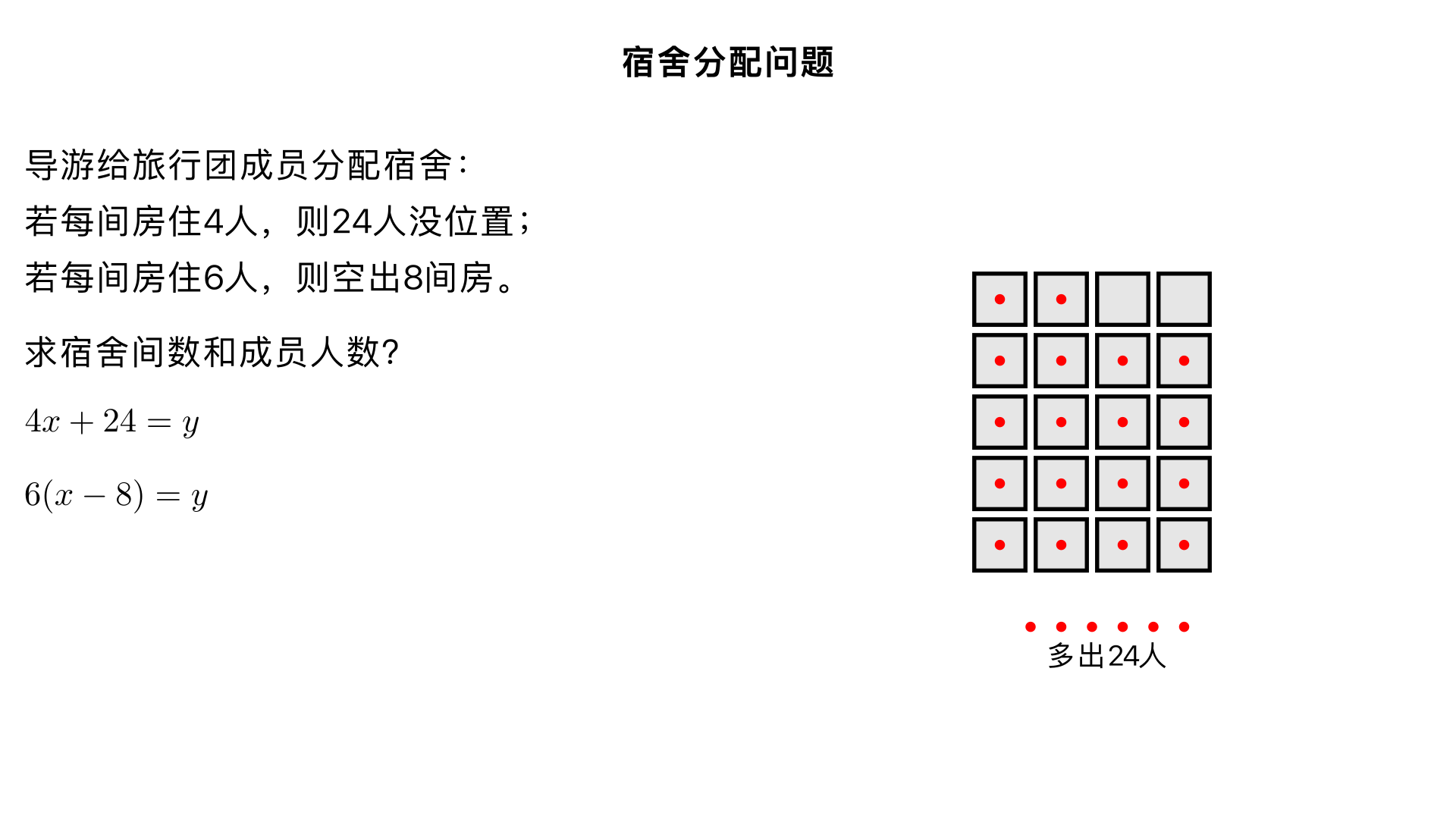
导游给某旅行团的成员分配宿会,如果每个房间住4人,则24人没有位置.如果每个房间住6人,则空出8个房间,求宿舍有多少间旅行团的成员有多少人
▶
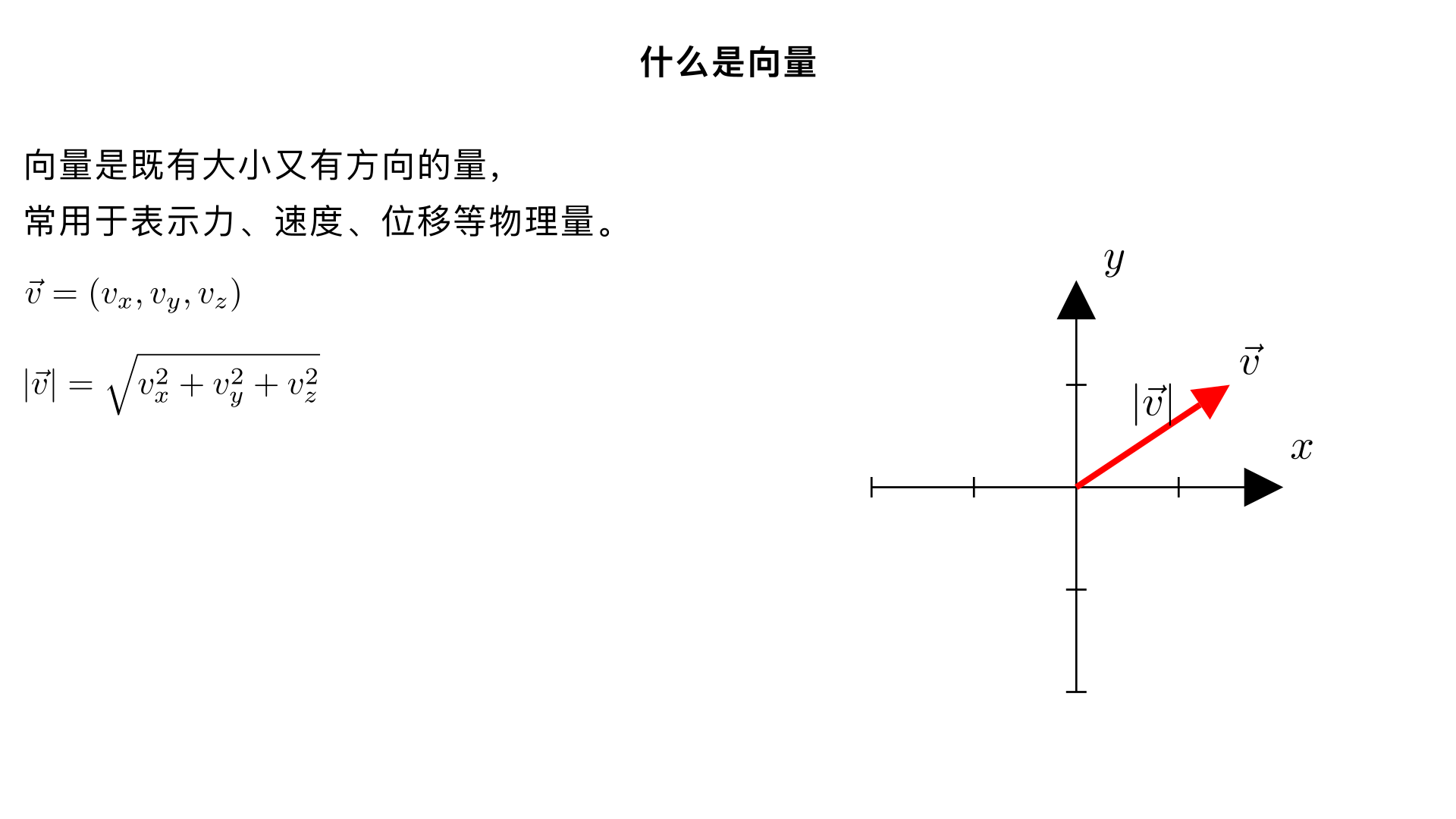
什么是向量
▶
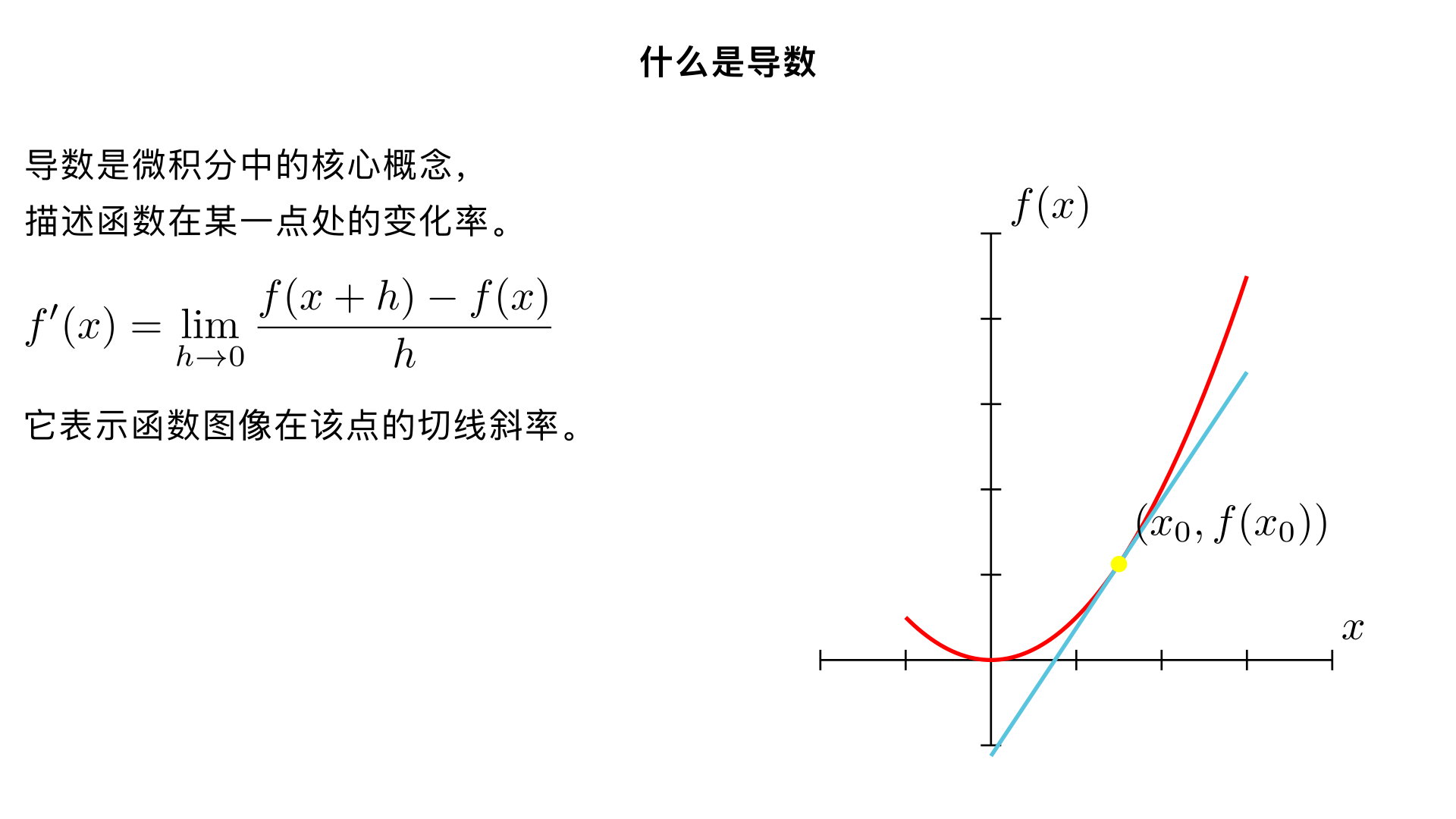
什么是导数
▶
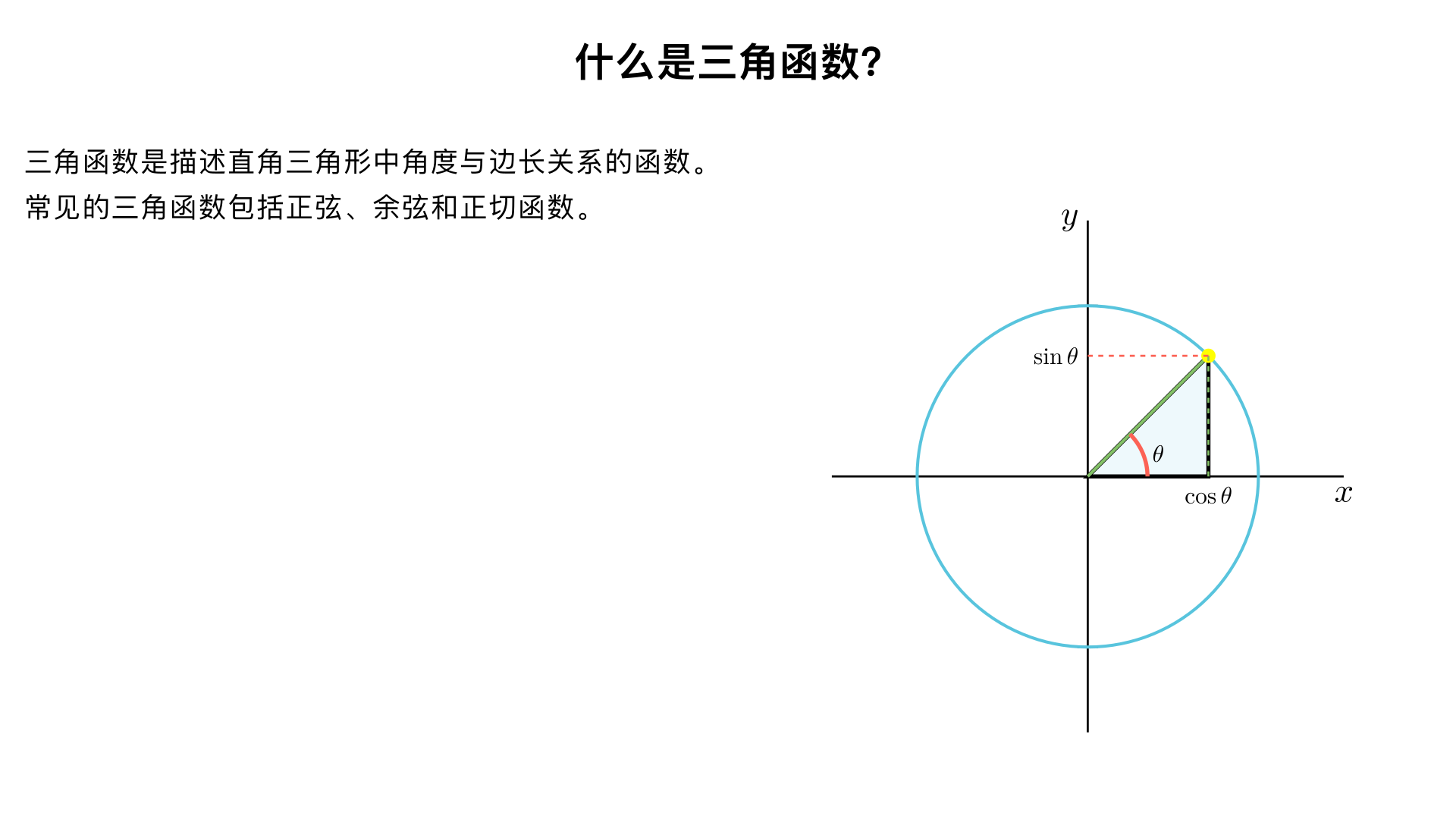
什么是三角函数
▶
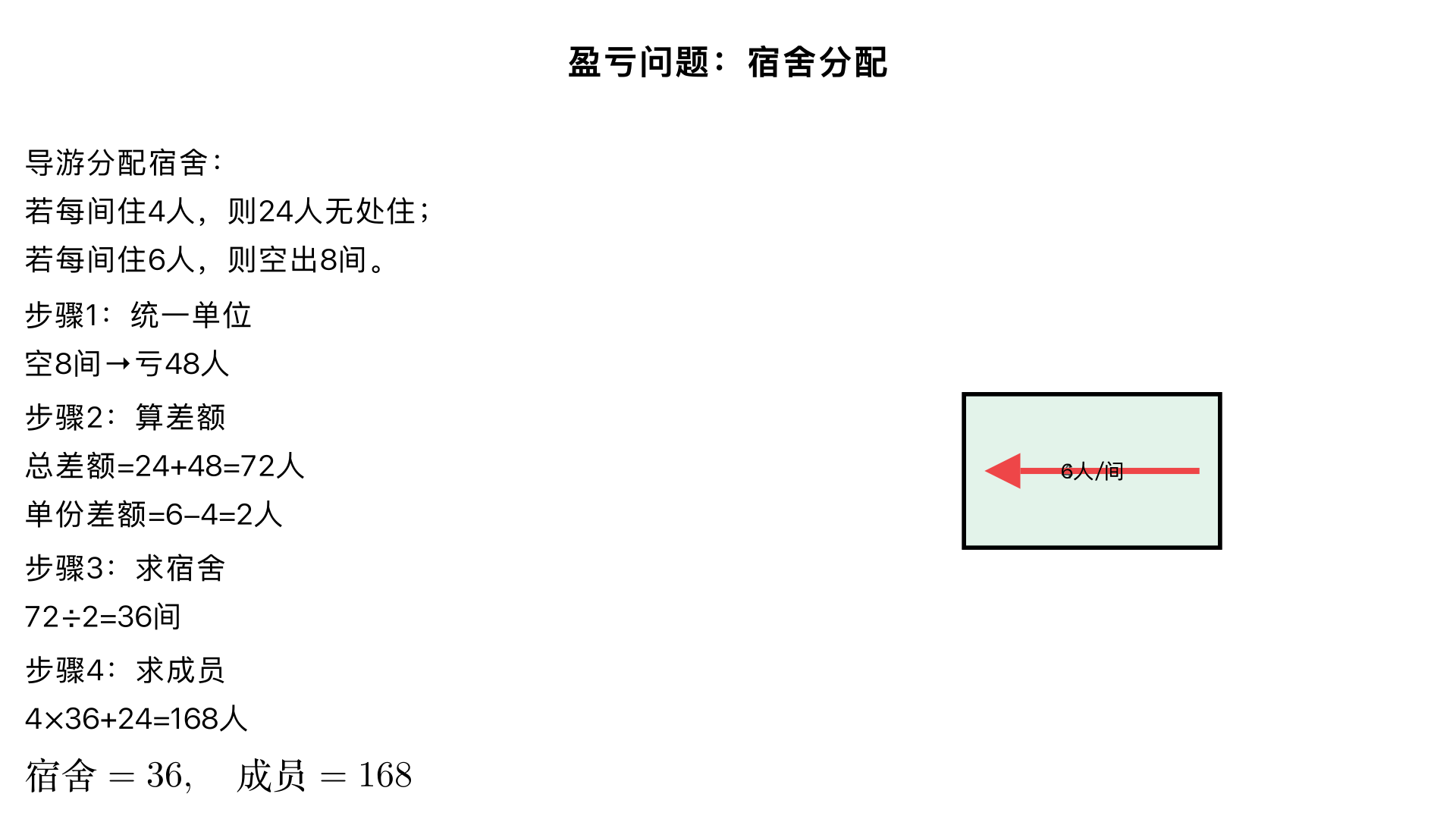
盈亏问题:导游给某旅行团的成员分配宿会,如果每个房间住4人,则24人没有位置.如果每个房间住6人,则空出8个房间,求宿舍有多少间旅行团的成员有多少人? 一、题型判断:盈亏问题(小学奥数 “盈亏问题之‘一盈一亏’” 核心子类) 这类题型的核心是通过两种不同的分配方案,先统一 “盈”(多余的人)和 “亏”(空房间对应的人数)的单位,再利用 “总差额 ÷ 单份差额” 求出分配份数(宿舍间数) ,解题关键是把 “空房间” 转化为 “缺少的床位(人数)”,本质是分配关系的平衡与差额计算,是小学奥数盈亏问题的高频必考题型。 二、解题过程(分 4 步:统一单位→算核心差额→求宿舍间数→求成员人数) 已知条件: 方案一(盈):每间住 4 人,24 人没位置(多余 24 人,即 “盈 24 人”); 方案二(亏):每间住 6 人,空出 8 个房间(空房间 = 缺少的床位,需转化为 “亏的人数”);核心逻辑:盈亏问题的核心公式是「分配份数 = 总差额 ÷ 单份差额」,先把 “空房间” 转化为人数,再计算总差额和单份差额,最终推导答案。 步骤 1:统一单位,把 “空房间” 转化为 “亏的人数” 每间住 6 人,空 8 个房间,说明这 8 个房间本可以住满,相当于 “少了 8 间房对应的人数”,即:亏的人数 = 每间住的人数 × 空房间数 = 6×8 = 48 人;(通俗理解:按方案二住,要住下所有人,还需要 48 人才能把空房间住满,相当于 “亏 48 人”) 步骤 2:计算总差额和单份差额 总差额(一盈一亏型):盈的人数 + 亏的人数 = 24 + 48 = 72 人;(理解:两种方案的人数差距的总和,就是能多容纳的总人数) 单份差额(每间住的人数差):方案二比方案一每间多住 = 6 - 4 = 2 人; 步骤 3:求宿舍间数(分配份数) 宿舍间数 = 总差额 ÷ 单份差额 = 72÷2 = 36 间;(理解:每间多住 2 人,总共能多容纳 72 人,所以一共有 36 间宿舍) 步骤 4:求旅行团成员总人数(两种方案验证,结果一致) 用方案一计算:总人数 = 每间人数 × 宿舍间数 + 盈的人数 = 4×36 + 24 = 144 + 24 = 168 人; 用方案二计算:总人数 = 每间人数 ×(宿舍间数 - 空房间数)= 6×(36 - 8)= 6×28 = 168 人; 三、反推验证(逐一对接条件,确认无误差) 验证方案一:36 间宿舍,每间住 4 人,能住 4×36=144 人,多余 24 人,144+24=168 人,与总人数一致 ✔️; 验证方案二:36 间宿舍,空 8 间,实际住 36-8=28 间,每间住 6 人,28×6=168 人,刚好住满,与总人数一致 ✔️; 差额逻辑验证:单份差额 2 人,36 间宿舍 ×2 人 = 72 人,刚好等于总差额(24+48),逻辑闭环 ✔️; 公式验证:完全符合盈亏问题「一盈一亏」的解题逻辑,计算过程无遗漏、无错误 ✔️; 四、最终结果 宿舍有 36 间,旅行团的成员有 168 人。
▶
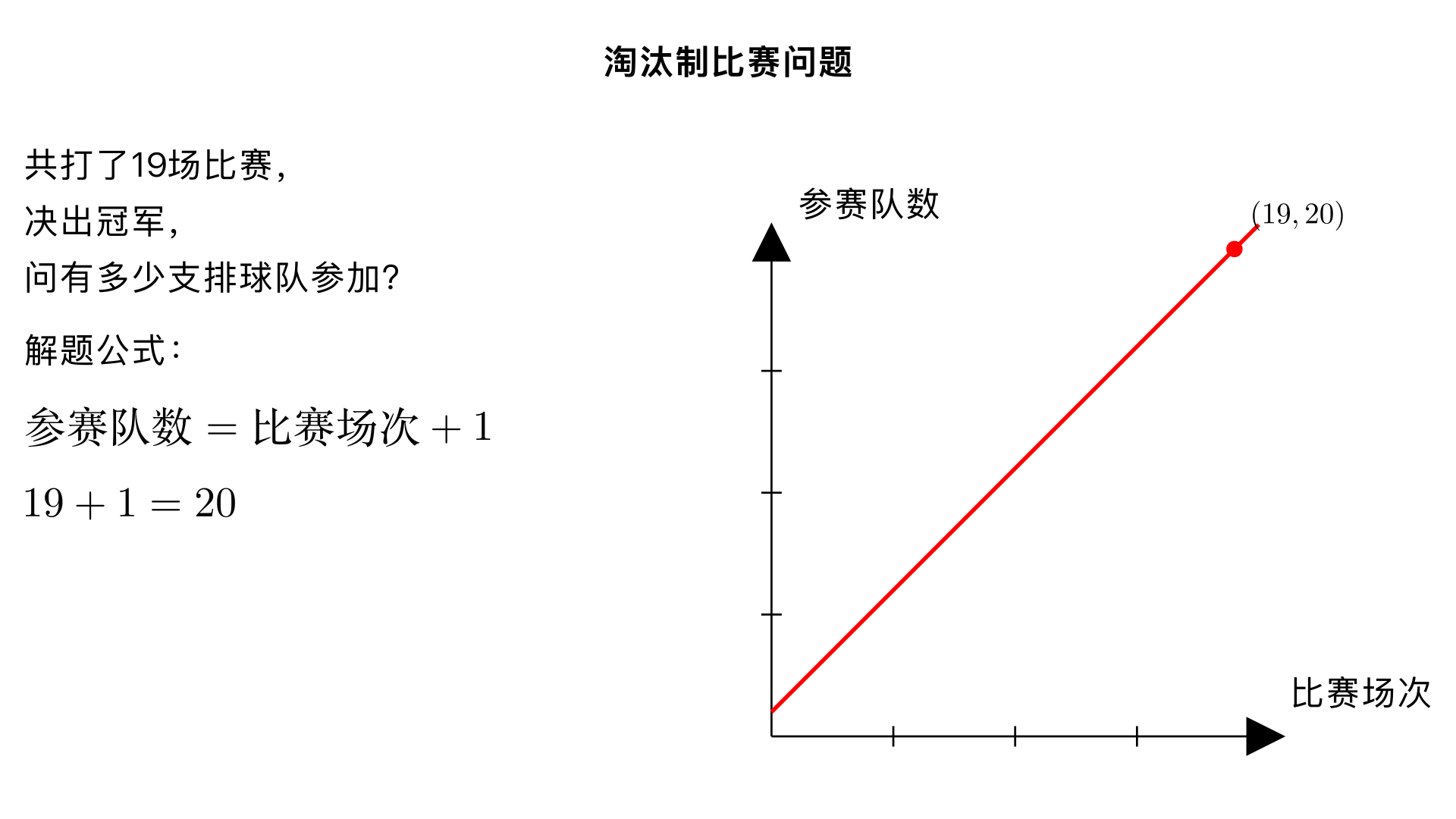
淘汰制比赛问题:在一次排球比赛中,采取陶汰制,共打了19场球,最后决出冠军,问有多少支排球队参加了这次排球比赛? 一、题型判断:淘汰制比赛问题(小学奥数 “比赛场次与参赛人数关系” 子类) 这类题型的核心是理解淘汰制的规则:每场比赛淘汰 1 支球队,最终决出冠军时,除冠军外所有球队都需被淘汰,解题关键是建立 “比赛场次 = 淘汰球队数” 的对应关系,本质是 “逻辑推理在比赛规则中的应用”。 二、解题过程(分 2 步:分析淘汰制核心逻辑→计算参赛人数) 已知条件: 比赛规则:淘汰制(每场比赛淘汰 1 支球队,无平局、无轮空特殊情况); 比赛总场次:19 场; 结果:决出 1 名冠军。 核心逻辑:淘汰制下,要决出冠军,必须淘汰掉除冠军外的所有球队。每打 1 场比赛,就淘汰 1 支球队,因此 “淘汰的球队总数 = 比赛总场次”。 步骤 1:计算淘汰的球队总数 因为每场比赛淘汰 1 支球队,共打了 19 场,所以淘汰的球队总数 = 19 支。 步骤 2:计算参赛总人数 参赛总人数 = 淘汰的球队数 + 冠军球队数(冠军未被淘汰),即:参赛总人数 = 19 + 1 = 20 支。 三、反推验证(核对逻辑与实际场景,确认结果无误) 逻辑验证:若有 20 支球队,决出冠军需淘汰 19 支球队,每场淘汰 1 支,因此需要打 19 场比赛,与题目给出的 “19 场” 完全一致 ✔️; 实例验证(小规模球队模拟): 若有 2 支球队,需打 1 场(淘汰 1 支,决出冠军),符合 “1 场 = 2-1”; 若有 3 支球队,需打 2 场(第一场淘汰 1 支,剩 2 支;第二场淘汰 1 支,决出冠军),符合 “2 场 = 3-1”; 规律:参赛球队数 = 比赛场次 + 1,因此 19 场 + 1=20 支,规律一致 ✔️; 反向验证:若参赛球队数为 20 支,无轮空情况下,比赛场次 = 20-1=19 场,与题目条件完全匹配,无逻辑矛盾 ✔️。 四、最终结果 参加这次排球比赛的排球队共有 20 支。
▶
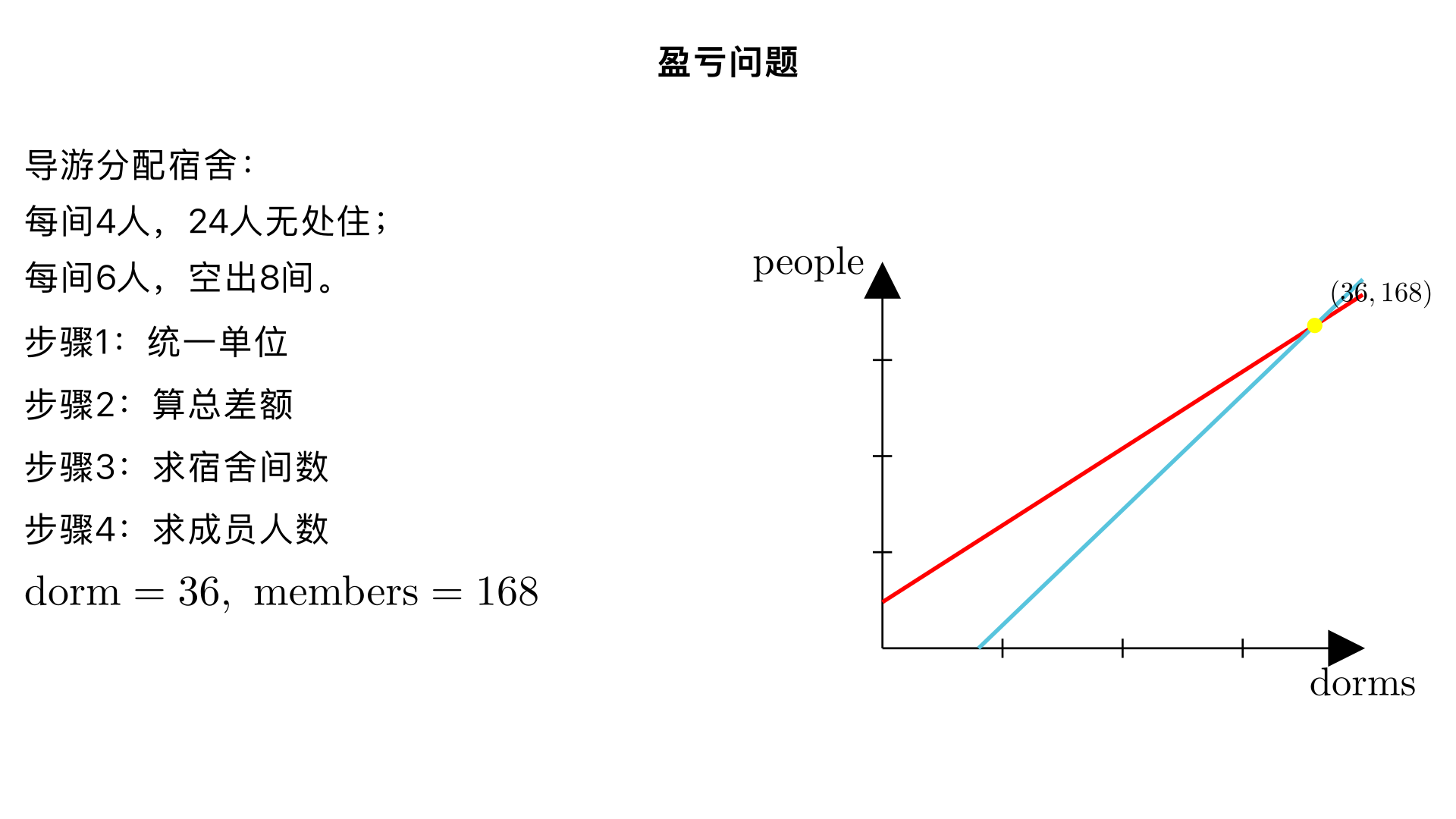
盈亏问题;导游给某旅行团的成员分配宿会,如果每个房间住4人,则24人没有位置.如果每个房间住6人,则空出8个房间,求宿舍有多少间旅行团的成员有多少人? 一、题型判断:盈亏问题(小学奥数 “盈亏问题之‘一盈一亏’” 子类) 这类题型的核心是通过两种不同的分配方案,找出 “盈”(多余的人)和 “亏”(空出房间对应的人数),利用 “总差额 ÷ 单份差额” 求出分配的份数(宿舍间数) ,解题关键是统一 “盈”“亏” 的单位(都转化为 “人数”),本质是 “分配关系的平衡与差额计算”。 二、解题过程(分 4 步:统一单位→算总差额→求宿舍间数→求成员人数) 已知条件: 方案一:每间住 4 人,多 24 人(盈:有 24 人没位置,是多余的人数); 方案二:每间住 6 人,空 8 个房间(亏:空房间意味着少了 “8 间房能住的人数”,需转化为人数);核心逻辑:先把 “空 8 个房间” 转化为 “少的人数”(亏数),再根据 “总差额 = 盈 + 亏”“单份差额 = 两种方案每间住的人数差”,求出宿舍间数,最后求总人数。 步骤 1:统一单位,把 “空房间” 转化为 “亏的人数” 每间住 6 人,空 8 个房间,说明少了 “8 间房能住的人数”,即:亏的人数 = 每间住的人数 × 空房间数 = 6×8 = 48 人;(理解:如果要让所有人住下,按方案二,还需要 48 人才能把空房间住满,相当于 “少了 48 人”) 步骤 2:计算总差额和单份差额 总差额(盈 + 亏):方案一多 24 人,方案二少 48 人,总差额 = 24 + 48 = 72 人; 单份差额(每间住的人数差):方案二比方案一每间多住 = 6 - 4 = 2 人; 步骤 3:求宿舍的间数 宿舍间数 = 总差额 ÷ 单份差额 = 72 ÷ 2 = 36 间;(理解:每间多住 2 人,总共能多容纳 72 人,所以有 36 间宿舍) 步骤 4:求旅行团的成员人数(用两种方案验证,结果一致) 用方案一计算:总人数 = 每间住的人数 × 宿舍间数 + 多余的人数 = 4×36 + 24 = 144 + 24 = 168 人; 用方案二计算:总人数 = 每间住的人数 ×(宿舍间数 - 空房间数)= 6×(36 - 8)= 6×28 = 168 人;(两种方案结果一致,说明计算正确) 三、反推验证(核对两种方案,确认所有条件都满足) 验证方案一:36 间房,每间住 4 人,能住 4×36=144 人,多 24 人,总人数 144+24=168 人 ✔️; 验证方案二:36 间房,空 8 间,实际住 36-8=28 间,每间住 6 人,总人数 28×6=168 人 ✔️; 差额逻辑验证:总差额 72 人,单份差额 2 人,36 间 ×2 人 = 72 人,刚好对应总差额,逻辑闭环 ✔️; 单位转化验证:空 8 间房 = 6×8=48 人(亏数),盈 24 + 亏 48=72,计算无误差 ✔️。 四、最终结果 宿舍有 36 间,旅行团的成员有 168 人。

▶
和差问题:桃树、梨树、苹果树共有59棵,桃树和梨树的总棵数比苹果树多23棵,桃树比梨树少1棵,三种树各有多少棵?

▶
和差问题:桃树、梨树、苹果树共有59棵,桃树和梨树的总棵数比苹果树多23棵,桃树比梨树少1棵,三种树各有多少棵? 一、题型判断:和差问题(小学奥数 “三量和差关系” 子类) 这类题型的核心是通过 “三个量的总数量” 和 “两两之间的数量关系”,逐步转化为两量和差问题,解题关键是先求出其中一个量的数量,再根据两两关系推导另外两个量,本质是 “数量关系的转化与和差公式的灵活应用”。 二、解题过程(分 3 步:转化两量关系→求单一量→推导其他量) 已知条件: 桃树(桃)+ 梨树(梨)+ 苹果树(苹)= 59 棵; 桃树 + 梨树 - 苹果树 = 23 棵; 梨树 - 桃树 = 1 棵(桃树比梨树少 1 棵);核心逻辑:先把 “桃树 + 梨树” 看成一个整体,与苹果树构成两量和差,求出苹果树和 “桃 + 梨” 的总数,再用两量和差求桃树、梨树各自数量。 步骤 1:求苹果树的棵数(转化两量和差) 设 “桃 + 梨” 为一个整体(记为 A),则: A + 苹 = 59(总棵数); A - 苹 = 23(桃梨总和比苹果树多 23 棵);根据和差公式:小数 =(和 - 差)÷2(苹果树是小数,因为 A 比苹多),可得:苹果树 = (59 - 23)÷ 2 = 36 ÷ 2 = 18 棵; 步骤 2:求桃树 + 梨树的总棵数 桃 + 梨 = 59 - 苹 = 59 - 18 = 41 棵; 步骤 3:求桃树、梨树各自的棵数 已知 “梨 - 桃 = 1 棵”,且 “桃 + 梨 = 41 棵”,再次用和差公式: 梨树(大数)=(和 + 差)÷2 =(41 + 1)÷2 = 42 ÷ 2 = 21 棵; 桃树(小数)=(和 - 差)÷2 =(41 - 1)÷2 = 40 ÷ 2 = 20 棵;(或:桃树 = 梨树 - 1 = 21 - 1 = 20 棵,结果一致) 三、反推验证(核对所有条件,确认无误差) 总棵数验证:20(桃)+ 21(梨)+ 18(苹)= 59 棵,与题目条件一致 ✔️; 桃梨总和与苹果树的关系验证:20+21=41 棵,41 - 18=23 棵,符合 “桃梨总和比苹果树多 23 棵” ✔️; 桃树与梨树的关系验证:21 - 20=1 棵,符合 “桃树比梨树少 1 棵” ✔️; 公式逻辑验证:两次应用和差公式,推导过程无漏洞,数量关系完全闭环 ✔️。 四、最终结果 桃树有 20 棵,梨树有 21 棵,苹果树有 18 棵。
▶
解卦——雷雨作解:脱险之道与善后智慧
▶