T
Teach Me AnythingTMA
Video History
Page 9 / 126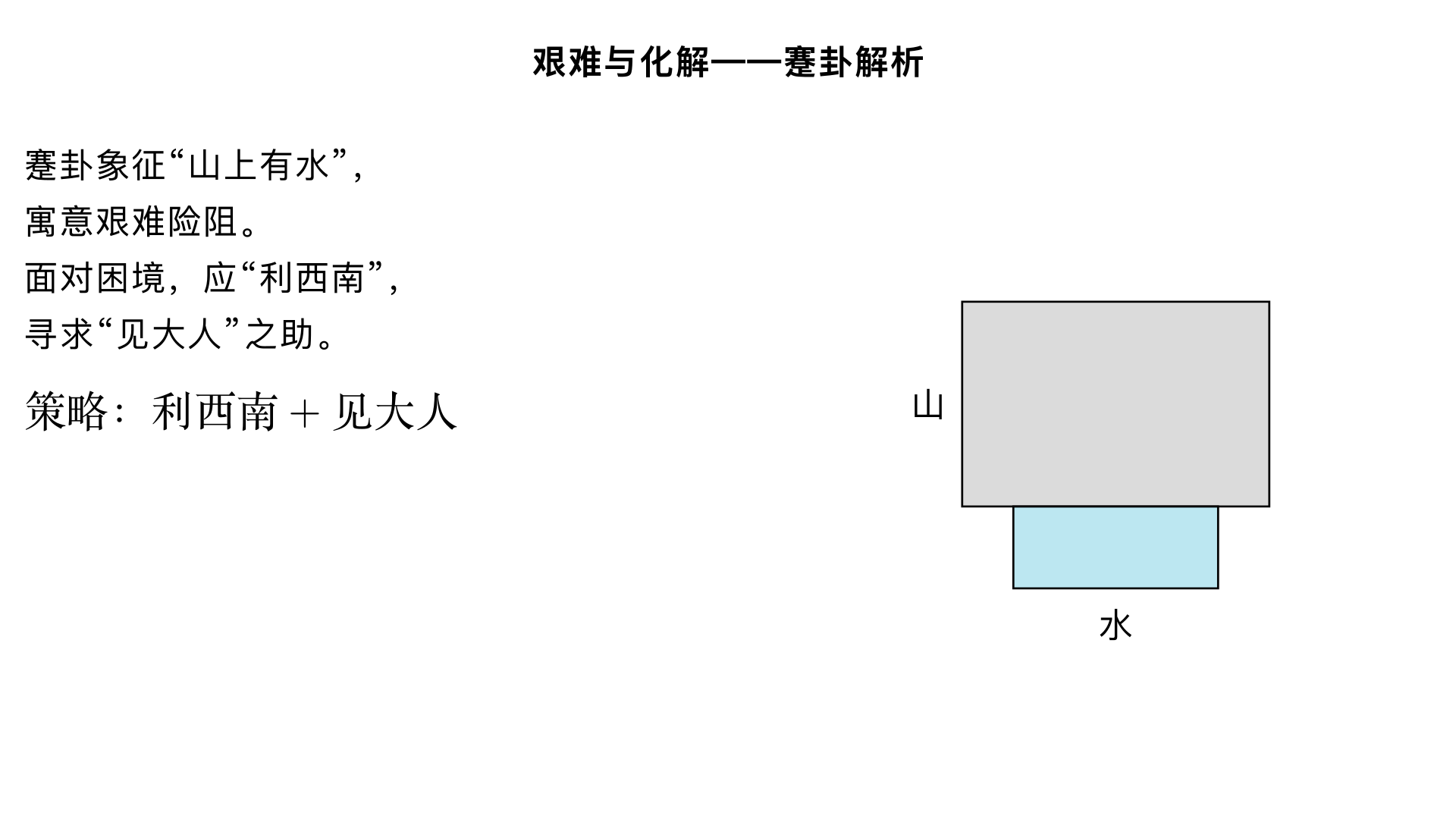
▶
艰难与化解——蹇卦解析 主要内容: 蹇卦:“山上有水”,讲解面对艰难时,“利西南”、“见大人”的应对策略。
▶
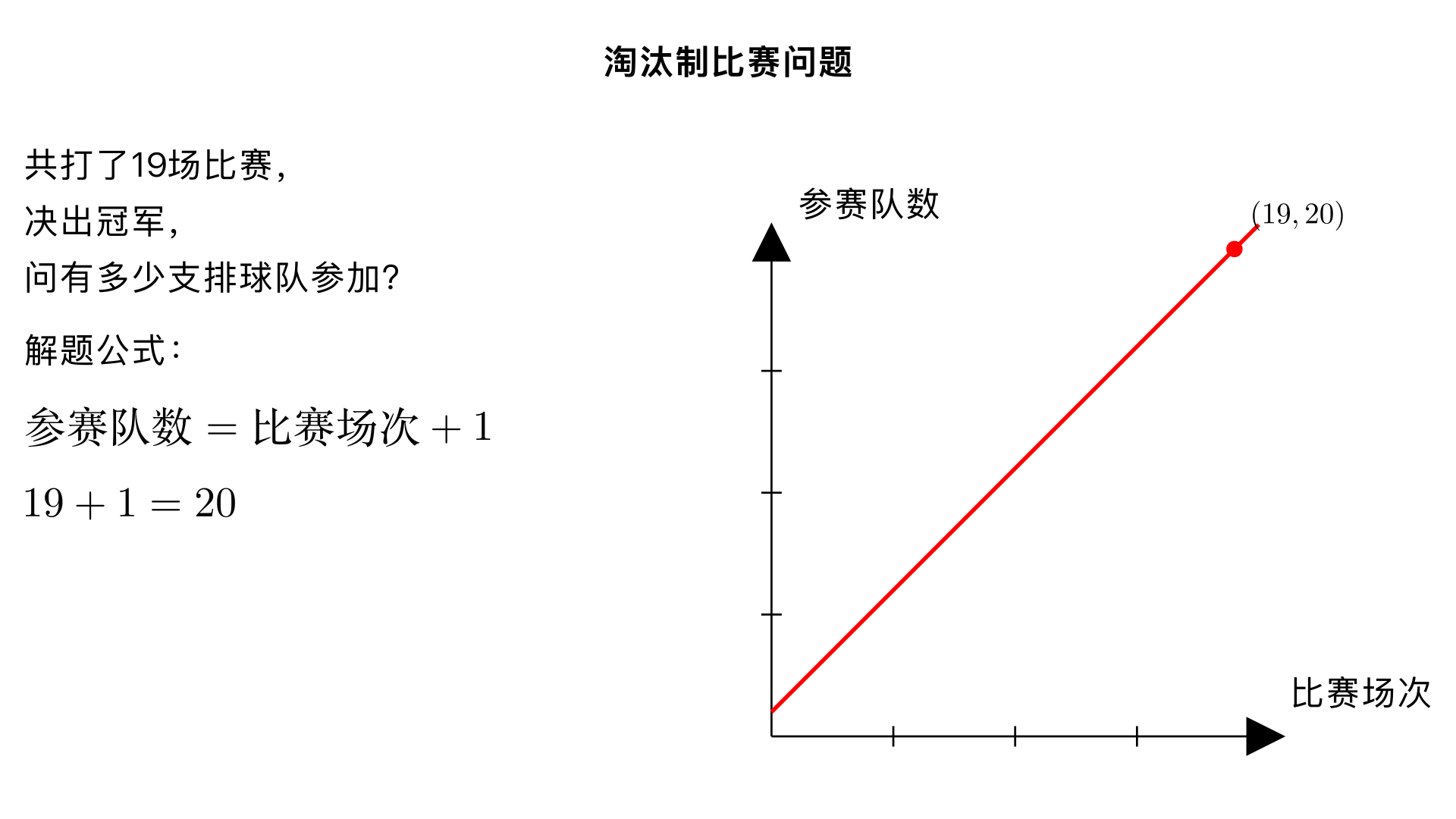
淘汰制比赛问题:在一次排球比赛中,采取陶汰制,共打了19场球,最后决出冠军,问有多少支排球队参加了这次排球比赛? 一、题型判断:淘汰制比赛问题(小学奥数 “比赛场次与参赛人数关系” 子类) 这类题型的核心是理解淘汰制的规则:每场比赛淘汰 1 支球队,最终决出冠军时,除冠军外所有球队都需被淘汰,解题关键是建立 “比赛场次 = 淘汰球队数” 的对应关系,本质是 “逻辑推理在比赛规则中的应用”。 二、解题过程(分 2 步:分析淘汰制核心逻辑→计算参赛人数) 已知条件: 比赛规则:淘汰制(每场比赛淘汰 1 支球队,无平局、无轮空特殊情况); 比赛总场次:19 场; 结果:决出 1 名冠军。 核心逻辑:淘汰制下,要决出冠军,必须淘汰掉除冠军外的所有球队。每打 1 场比赛,就淘汰 1 支球队,因此 “淘汰的球队总数 = 比赛总场次”。 步骤 1:计算淘汰的球队总数 因为每场比赛淘汰 1 支球队,共打了 19 场,所以淘汰的球队总数 = 19 支。 步骤 2:计算参赛总人数 参赛总人数 = 淘汰的球队数 + 冠军球队数(冠军未被淘汰),即:参赛总人数 = 19 + 1 = 20 支。 三、反推验证(核对逻辑与实际场景,确认结果无误) 逻辑验证:若有 20 支球队,决出冠军需淘汰 19 支球队,每场淘汰 1 支,因此需要打 19 场比赛,与题目给出的 “19 场” 完全一致 ✔️; 实例验证(小规模球队模拟): 若有 2 支球队,需打 1 场(淘汰 1 支,决出冠军),符合 “1 场 = 2-1”; 若有 3 支球队,需打 2 场(第一场淘汰 1 支,剩 2 支;第二场淘汰 1 支,决出冠军),符合 “2 场 = 3-1”; 规律:参赛球队数 = 比赛场次 + 1,因此 19 场 + 1=20 支,规律一致 ✔️; 反向验证:若参赛球队数为 20 支,无轮空情况下,比赛场次 = 20-1=19 场,与题目条件完全匹配,无逻辑矛盾 ✔️。 四、最终结果 参加这次排球比赛的排球队共有 20 支。
▶
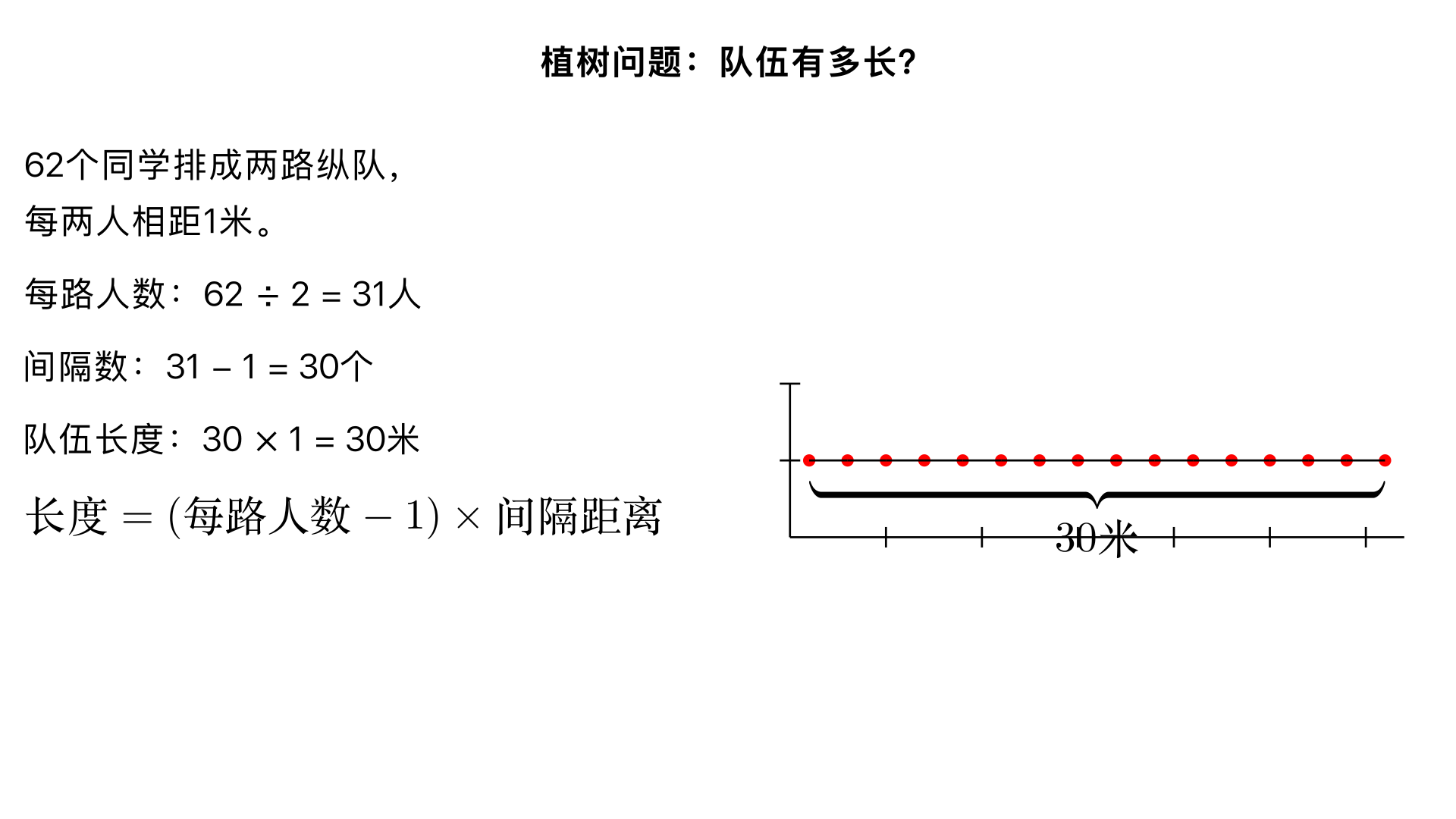
植树问题:学校组织同学去郊游,三(1)班62个同学排成两路纵队前进,每两个同学之间相距1米,这支队伍有多长? 一、题型判断:植树问题(小学奥数 “不封闭路线植树之两端都有人” 子类) 这类题型的核心是明确 “人数” 与 “间隔数” 的关系,在不封闭的纵队排列中,间隔数 = 每路人数 - 1,再结合每个间隔的长度计算队伍总长度,本质是 “点数与段数的数量关系应用”。 二、解题过程(分 3 步:计算每路人数→求间隔数→算队伍长度) 已知条件: 总人数:62 人,排成两路纵队; 间隔距离:每两个同学之间相距 1 米; 核心关系:纵队排列中,间隔数 = 每路人数 - 1(因为两端都站人,间隔数比人数少 1)。 步骤 1:计算每路纵队的人数 两路纵队人数相等,因此每路人数 = 总人数 ÷ 2\(62 ÷ 2 = 31\)(人) 步骤 2:计算每路纵队的间隔数 根据 “两端都有人,间隔数 = 人数 - 1”,可得:间隔数 = \(31 - 1 = 30\)(个) 步骤 3:计算队伍的长度 队伍长度 = 间隔数 × 每个间隔的距离\(30 × 1 = 30\)(米) 三、反推验证(核对逻辑与计算,确认结果无误) 人数与间隔数验证:每路 31 人,相邻两人 1 个间隔,从第 1 人到第 31 人,中间的间隔数确实是 \(31-1=30\) 个,符合 “两端都有点,段数 = 点数 - 1” 的规律 ✔️。 长度计算验证:30 个间隔,每个间隔 1 米,总长度 \(30×1=30\) 米,计算无误差 ✔️。 整体逻辑验证:62 人分两路,每路 31 人,队伍长度由间隔数决定,而非人数,若误算成 “31×1=31 米” 就会出错,此解法避开了这个常见误区 ✔️。 四、最终结果 这支队伍的长度是 30 米。
▶
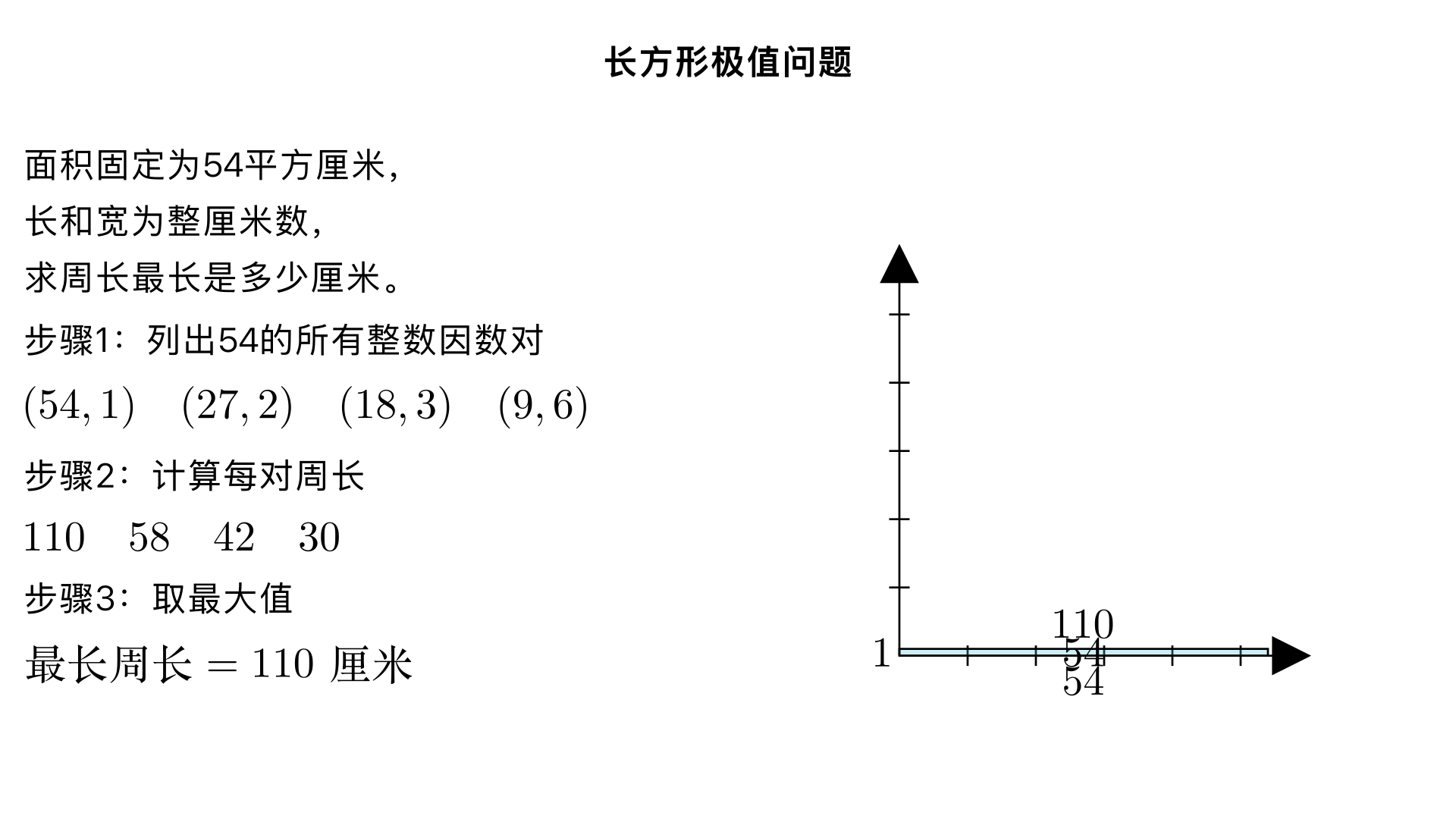
长方形极值问题:一个长方形的面积是54平方厘米,而且长和宽都是整厘米数,这个长方形的周长最长是多少厘米? 一、题型判断:长方形极值问题(小学奥数 “长方形面积与周长关系” 子类) 这类题型的核心是利用 “长方形面积固定时,长和宽的差值越大,周长越长;差值越小,周长越短” 的规律,通过枚举面积的所有整数因数组合,计算对应周长并找出最大值,本质是因数分解与周长公式的结合应用。 二、解题过程(分 3 步:因数分解→计算各组合周长→找出最大值) 已知条件: 长方形面积 = 54 平方厘米; 长和宽都是整厘米数(长 ≥ 宽); 长方形周长公式:周长 = (长 + 宽)× 2。 核心逻辑:面积固定时,长和宽的差越大,周长就越长,因此需要先找出 54 的所有整数因数对,再计算每对因数对应的周长。 步骤 1:对 54 进行因数分解,找出所有长和宽的组合 根据 \(长方形面积=长×宽\),列出 54 的所有整数因数对(长≥宽): \(54 = 54 × 1\) → 长 54cm,宽 1cm \(54 = 27 × 2\) → 长 27cm,宽 2cm \(54 = 18 × 3\) → 长 18cm,宽 3cm \(54 = 9 × 6\) → 长 9cm,宽 6cm 步骤 2:计算每组长和宽对应的周长 长 54cm,宽 1cm:周长 = \((54+1)×2 = 55×2 = 110\) 厘米 长 27cm,宽 2cm:周长 = \((27+2)×2 = 29×2 = 58\) 厘米 长 18cm,宽 3cm:周长 = \((18+3)×2 = 21×2 = 42\) 厘米 长 9cm,宽 6cm:周长 = \((9+6)×2 = 15×2 = 30\) 厘米 步骤 3:找出周长的最大值 对比四组周长:\(110>58>42>30\)因此,周长最长为 110 厘米。 三、反推验证(核对规律与计算,确认结果无误) 规律验证:长和宽的差值越大,周长越长。 54 和 1 的差值:\(54-1=53\) 27 和 2 的差值:\(27-2=25\) 差值最大的组合(54,1)对应周长最长,符合 “面积固定,差大周长大” 的规律 ✔️。 计算验证: 面积验证:\(54×1=54\) 平方厘米,与题目条件一致 ✔️; 周长验证:\((54+1)×2=110\) 厘米,计算过程无误差 ✔️。 完整性验证:已枚举 54 的所有整数因数对,没有遗漏组合,确保找到的是最大值 ✔️。 四、最终结果 这个长方形的周长最长是 110 厘米
▶
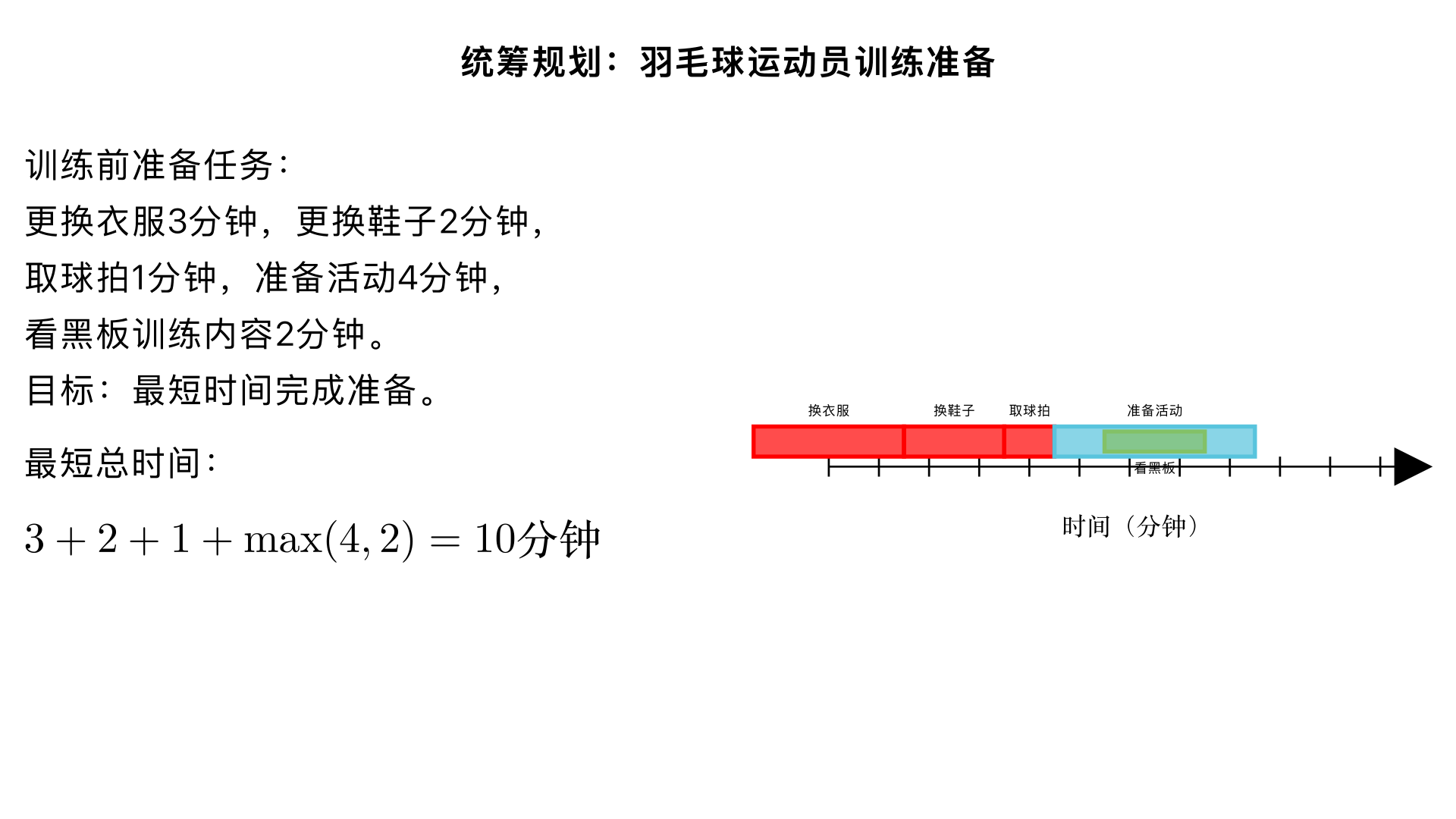
统筹规划:羽毛球运动员每次训练时,更换衣服要用3分钟,更换鞋子要用2分钟,取球拍要1分钟,准备活动要4分钟,看黑板上的训练内容要2分钟。羽毛球运动员怎样用尽可能短的时间投入训练最短的时间是多少? 一、题型判断:统筹规划问题(小学奥数 “时间优化” 子类) 这类题型的核心是通过合理安排操作顺序,找出可以并行进行的步骤,利用空闲时间完成其他任务,从而缩短总耗时。解题关键是区分 “必须独立完成的步骤” 和 “可以同步进行的步骤”,本质是时间资源的最优分配。 二、解题过程(分 2 步:梳理步骤关系→设计最优流程计算时间) 已知条件: 更换衣服:3 分钟; 更换鞋子:2 分钟; 取球拍:1 分钟; 准备活动:4 分钟; 看黑板训练内容:2 分钟;核心逻辑:分析各步骤的依赖关系,准备活动期间不需要专注操作,可以同步完成看黑板训练内容,从而节省时间。 步骤 1:区分 “独立步骤” 和 “可并行步骤” 必须依次独立完成的准备步骤(无空闲时间,需按顺序操作):更换衣服→更换鞋子→取球拍这三步的总耗时 = 3 + 2 + 1 = 6 分钟 可并行的步骤:准备活动(4 分钟)和看黑板训练内容(2 分钟)看黑板训练内容无需动手,可在准备活动时同步完成,且 2 分钟<4 分钟,完全可以覆盖,无需额外耗时。 步骤 2:计算最短总时间 最优流程:更换衣服(3 分钟)→ 更换鞋子(2 分钟)→ 取球拍(1 分钟)→ 准备活动(4 分钟,同步看训练内容 2 分钟)最短总时间 = 独立步骤总耗时 + 并行步骤中较长的耗时= 6 + 4 = 10 分钟 三、反推验证(核对流程合理性,确认无时间浪费) 并行操作有效性验证:准备活动需要 4 分钟,看训练内容只需要 2 分钟,在准备活动的前 2 分钟就可以完成看内容的任务,剩余 2 分钟继续做准备活动,没有额外增加时间 ✔️; 总时间对比验证:若不并行操作,总耗时 = 3+2+1+4+2 = 12 分钟;并行后节省了 2 分钟,10 分钟为最短耗时 ✔️; 逻辑顺序验证:步骤顺序无冲突(先换衣鞋、取球拍,再做准备活动),符合训练前的实际操作流程,没有颠倒顺序的不合理情况 ✔️; 时间计算验证:3+2+1+4=10 分钟,计算过程无误差 ✔️。 四、最终结果 最优安排:先更换衣服→更换鞋子→取球拍,然后做准备活动(同时看黑板上的训练内容);最短投入训练的时间是 10 分钟。
▶
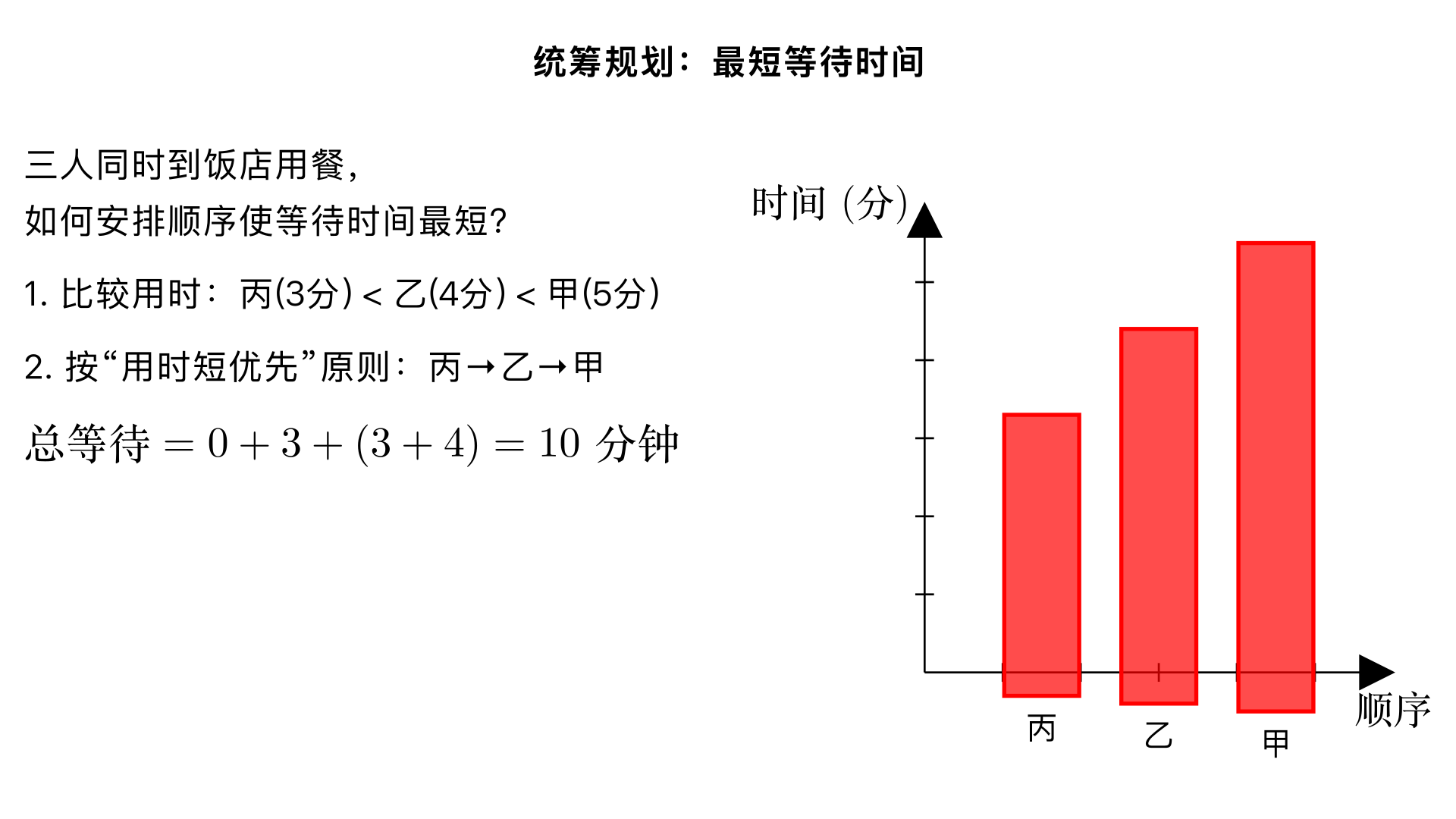
统筹规划:甲乙丙三人同时到一家饭店吃饭,甲吃面条要等5分钟,乙吃水饺要等4分钟,丙吃鸡蛋炒饭要等3分钟。怎样安排才能使他们三人等待的时间最短? 一、题型判断:统筹规划问题(小学奥数 “排队等候时间优化” 子类) 这类题型的核心是通过合理安排服务顺序,减少所有人的等待时间总和。解题关键是遵循 **“用时短的任务优先进行”** 原则,让等待时间短的人先接受服务,从而降低后续人员的累计等候时长,本质是时间资源的最优分配。 二、解题过程(分 2 步:确定最优顺序→计算最短等待时间总和) 已知条件: 甲吃面条需等 5 分钟,乙吃水饺需等 4 分钟,丙吃鸡蛋炒饭需等 3 分钟; 等待时间的计算:每个人的等待时间 = 自己开始用餐前,前面所有人的用餐准备时间之和; 目标:让三人等待的总时间最短。 步骤 1:确定最优服务顺序 比较三人的等待时长(即用餐准备时长):\(3分钟<4分钟<5分钟\)根据 “用时短优先” 原则,最优顺序为:丙先吃→乙其次→甲最后 步骤 2:计算等待时间总和 我们分角色计算每个人的等待时间,再求和: 丙用餐时:丙是第一个,无需等待,等待时间为 0 分钟;乙和甲需要等丙的 3 分钟,两人的等待时间各累计 3 分钟。 乙用餐时:乙的等待时间为丙的准备时间,即 3 分钟;甲需要再等乙的 4 分钟,甲的等待时间累计 \(3+4=7\) 分钟。 甲用餐时:甲的等待时间为丙 + 乙的准备时间,即 \(3+4=7\) 分钟。 等待时间总和 = 丙的等待时间 + 乙的等待时间 + 甲的等待时间= \(0 + 3 + 7 = 10\) 分钟 注:如果题目问 “从开始到三人都用餐的总时长”,则是 \(3+4+5=12\) 分钟;小学奥数中此类题默认求等待时间总和。 三、反推验证(对比其他顺序,确认最优) 验证最优顺序的合理性若顺序改为 “乙→丙→甲”:等待时间总和 = \(0 + 4 + (4+3) = 11\) 分钟,比最优顺序长;若顺序改为 “甲→乙→丙”:等待时间总和 = \(0 + 5 + (5+4) = 14\) 分钟,耗时更长;结论:丙→乙→甲的顺序等待时间总和最短(10 分钟)。 逻辑验证用时短的人先用餐,能减少后续两人的等待时长,符合 “短任务优先” 的统筹原则;等待时间计算无重复、无遗漏,每个人的等待时间都是前面人的准备时间之和,逻辑正确 ✔️。 四、最终结果 最优安排顺序:丙先吃鸡蛋炒饭→乙再吃水饺→甲最后吃面条;三人等待的时间总和最短为 10 分钟。
▶
睽卦——异中求同:社会和解的辩证智慧 一、卦序逻辑:从家人到睽违的深刻转折 1. 《序卦传》的辩证法 “家道穷必乖,故受之以睽。睽者,乖也。” 家人卦(风火家人)讲家庭和谐 → 但家道发展到极端(穷)则会产生乖离 金景芳释:此揭示“物极必反”规律,和谐中已潜伏矛盾 2. 与家人卦的反对关系 家人卦(䷤):风火家人 → 家人卦旋转180°即成睽卦(䷥) 在《周易》中称“综卦”或“反对卦”,象征事物的正反两面 体现《周易》核心智慧:见同必思异,见合必思分 二、睽卦(火泽睽)卦象的矛盾与统一 1. “上火下泽”的背离之象 基本卦象:上离火,下兑泽 → 火炎上,泽润下,二者背道而驰 自然象征:如沼泽上的野火,火势向上,水汽向下 人情象征:心志相背,意见不合,如《诗经》“兄弟阋于墙” 2. 卦中隐含的交通之机 金景芳深刻洞察:睽卦看似背离,实则内藏“异中求同”的契机 离为中女,兑为少女 → 二女同居(同性相斥) 但离为明,兑为悦 → 若能“文明以悦”,可化解矛盾 六爻中三、四、五爻构成互坎(水)→ 水能调和火泽 3. 睽卦的积极意义 卦辞:“睽,小事吉” “小事吉”:在乖离时,从小事做起可获吉祥 如破冰从微笑、问候开始 《彖传》:“天地睽而其事同也,男女睽而其志通也,万物睽而其事类也” 将“睽”(差异)提升为宇宙普遍现象 差异恰是合作的前提(如男女差异成就婚姻) 三、彖传精解:睽而能合的宇宙人生哲学 “睽,火动而上,泽动而下。二女同居,其志不同行。 说而丽乎明,柔进而上行,得中而应乎刚,是以小事吉。 天地睽而其事同也,男女睽而其志通也,万物睽而其事类也。睽之时用大矣哉!” 1. “火动而上,泽动而下”的物理描述 直观展现背离现象 金景芳引申:如团队中有人激进(火向上),有人保守(泽向下) 2. “二女同居,其志不同行”的人情观察 离为中女,兑为少女,同处一卦如姐妹同居 “志不同行”:心思不同,难以同步 历史类比:武则天与太平公主母女相忌 3. “说而丽乎明”的化解之道 下兑为悦(说),上离为明 心理机制:以愉悦心态附丽于光明目标 如国共合作抗日,虽理念不同,但共享民族大义(明) 4. “柔进而上行,得中而应乎刚”的卦爻结构 指六五爻:柔爻进居尊位,得中道而与九二刚爻相应 象征:以柔和解,居中调停,得强援支持 历史例证:蔺相如避让廉颇,以柔克刚,终得刎颈之交 5. 宇宙论的升华:“天地睽而其事同也” 三重类比: 天地睽:天高地卑,形态相背 → 但共成化育之事(同) 男女睽:生理心理差异 → 但志趣可通(通) 万物睽:形形色色各不相同 → 但事理相类(类) 金景芳哲学阐发: 这是《周易》差异哲学的巅峰表述 差异不是问题,拒绝在差异中寻找共同点才是问题 与《庄子》“齐物论”异曲同工:承认差异而追求和谐 6. “睽之时用大矣哉!”的实用赞叹 睽卦的时用价值太重大了! 金景芳:此赞语在《彖传》中少见,仅用于特别重要的卦(如坎、蹇、睽),凸显“和解”智慧的价值 四、大象传:“同而异”的处世智慧 “上火下泽,睽。君子以同而异。” 短短四字,蕴含极深智慧 1. “同而异”的三种解读 第一种(主流):在相同中见差异(保持独立思考) 如孔子“和而不同”,不盲目附和 第二种(操作):为达到同(合作)而承认异(差异) 如统一战线,求同存异 第三种(境界):同与异辩证统一 如《中庸》“万物并育而不相害,道并行而不相悖” 2. 现代应用 国际关系:和平共处五项原则(求同存异) 企业管理:团队多样性管理(同而异) 文化冲突:文明对话而非文明冲突 五、爻辞精析:从乖离到和解的心理历程 睽卦六爻展现了一个完整的“冲突-和解”过程,每爻都是一步心理转变。 1. 初九:悔亡。丧马勿逐,自复。见恶人,无咎。 “丧马勿逐”寓言:马跑了别追,自己会回来 睽初智慧: 对轻微的背离(丧马),不激烈对抗(勿逐) 给对方空间,信任其“自复” “见恶人,无咎”:主动会见与己不合者,可免咎 如周恩来万隆会议主动与不同阵营交往 爻象:初九阳刚居睽始,与九四无应,但守正不躁 2. 九二:遇主于巷,无咎。 “遇主于巷”:在巷中遇见主人(指六五) 象征:在非常规场合(巷非大堂)遇到关键人物 爻位:九二刚中,与六五正应但被阻隔(因睽违) 和解策略: 放下形式,不拘常规 主动创造非正式沟通机会 历史类比:萧何月下追韩信,不拘礼节 3. 六三:见舆曳,其牛掣,其人天且劓,无初有终。 生动比喻: “舆曳”:车被往后拉 “牛掣”:牛往前拽 “天且劓”:遭额刺(天)割鼻(劓)之刑 象征:身处矛盾夹缝,备受伤害 爻象:六三阴柔失正,处二阳之间(九二、九四),上下受制 “无初有终”:开始艰难,终有好结果 如苏武羁留匈奴,始受困,终归汉 金景芳释:此爻警示,和解过程中可能有牺牲,但坚持可得善终 4. 九四:睽孤,遇元夫,交孚,厉无咎。 全卦转折点:“元夫”是关键 爻辞分解: “睽孤”:乖离孤独(九四处六三、六五两阴之间,孤独无应) “遇元夫”:遇到阳刚丈夫(指初九,同德相应) “交孚”:以诚信相交 爻象精析:九四与初九同为阳爻,本不应,但在睽卦特殊情境下,因“同德”而“交孚” “厉无咎”:虽有危险但无咎害 历史印证: 管仲与鲍叔牙,虽各事其主(公子纠与小白),但“交孚”终成知己 马克思与恩格斯,背景不同但“遇元夫” 5. 六五:悔亡。厥宗噬肤,往何咎? “厥宗噬肤”:其宗族如咬嫩肉般容易融合 爻象:六五柔中居尊,下应九二 睽而能合的条件: 居尊位(有权威) 行中道(不偏激) 有正应(得支持) “往何咎”:前往和解有何咎害? 历史典范:唐太宗处理魏征(原为太子建成谋士),化敌为臣,创贞观之治 6. 上九:睽孤,见豕负涂,载鬼一车,先张之弧,后说之弧。匪寇婚媾,往遇雨则吉。 最生动的一爻,展现“疑心生暗鬼”到“真相大白”全过程 心理戏剧四幕: 幻觉阶段:“见豕负涂”——看见猪满身污泥(疑心丑化对方) 疑惧阶段:“载鬼一车”——以为一车鬼怪(恐惧放大) 敌对阶段:“先张之弧”——先拉开弓(准备攻击) 和解阶段:“后说之弧”——后放下弓(解除戒备) 真相:“匪寇婚媾”——不是强盗,是求婚队伍 条件:“往遇雨则吉”——前往遇雨则吉(雨象征阴阳和合) 爻象:上九处睽极,疑心最重,但终与六三相应(真相是“婚媾”) 金景芳深刻阐发: 此爻揭示:多数矛盾源于误解(豕非鬼,婚媾非寇) 和解需要“遇雨”——外部契机或内心顿悟 如将相和,始而疑,终而合 六、睽卦的和解智慧总论 1. 和解三阶段: 初级阶段(初、二爻):不追不逐,主动接触 中级阶段(三、四爻):忍受煎熬,诚信相交 高级阶段(五、上爻):权威调解,破除幻觉 2. 四种和解策略: 空间策略(初九):勿逐自复,给缓冲空间 场合策略(九二):巷中遇主,非正式沟通 诚信策略(九四):交孚元夫,以诚化异 权威策略(六五):厥宗噬肤,领导调解 3. 心理障碍破除: 上九爻揭示:矛盾常是“疑心生暗鬼” 和解需要“遇雨”——冷静期或第三方介入 4. 金景芳哲学总结:睽卦是儒家“和而不同”思想的易学展开,承认差异的必然性,但更强调在差异中寻找共性。“睽之时用大矣哉”的赞叹,表明《周易》将“和解能力”视为最重要的生存智慧之一。
▶
家人卦——风火齐家:家庭伦理的易学基石 一、卦序背景:从黑暗到重建 1. 明夷之后的必然转向 《序卦传》逻辑链:“夷者,伤也。伤于外者必反于家,故受之以家人。” 明夷卦(地火明夷)象征外部世界的伤害与黑暗 → 创伤后自然回归家庭寻求庇护与重建 金景芳指出:此卦序深刻反映儒家“家国同构”思想,家庭是社会的最小稳定单元 2. 下经人伦体系的关键环节 咸恒(夫妇)→ 遁大壮(进退)→ 晋明夷(顺逆)→ 家人(齐家) 家人卦是“修身齐家治国平天下”链条中的核心一环 金景芳强调:儒家政治哲学始于家庭伦理,“家齐而后国治” 二、家人卦(风火家人)卦象的哲学深意 1. “风自火出”的独特卦象 基本卦象:上巽风,下离火 → 风从火出 物理逻辑:火燃烧产生热气上升,带动空气流动成风 金景芳哲学诠释: 离火象征内在的光明、温暖与情感(家的精神内核) 巽风象征外在的教化、传播与影响(家风的扩散) 核心命题:有内在的真情(火),才有外在的教化(风)→ “有诸内必形诸外” 2. 六爻结构的家庭象征 初、上爻为阳,中间四爻为阴 → 如房屋结构:阳爻为梁柱(初基、上顶),阴爻为空间(家庭成员) 六二阴爻居内卦中位 → 女正位乎内(主妇) 九五阳爻居外卦中位 → 男正位乎外(家主) 金景芳特别指出:此卦爻位完美对应传统家庭角色分工 3. 与明夷卦的象数关联 明夷卦(䷣):地火明夷 → 明入地中,黑暗困顿 家人卦(䷤):风火家人 → 火生风出,内部重建 二卦下卦皆为离火(光明),但上卦一为坤土(压抑),一为巽风(疏通) 象征:同样的内在光明,在不同外部环境下,或受压抑,或得发扬 三、彖传精解:儒家家庭伦理总纲 “家人,女正位乎内,男正位乎外。男女正,天地之大义也。 家人有严君焉,父母之谓也。父父,子子,兄兄,弟弟,夫夫,妇妇,而家道正。正家而天下定矣。” 1. “女正位乎内,男正位乎外”的经典定位 卦象依据: 六二阴爻居内卦(下离)中位 → 女正内 九五阳爻居外卦(上巽)中位 → 男正外 金景芳历史语境阐释: 非现代意义的性别歧视,而是农业社会的角色分工 “内”指家庭内部事务管理,“外”指社会生产与公共事务 重点在“正位”——各安其位,各尽其责 与《诗经》印证:“无非无仪,唯酒食是议”(女性内职),“召彼仆夫,谓之载矣”(男性外事) 2. “男女正,天地之大义也”的宇宙论提升 将家庭伦理上升至“天地之道”: 乾天为阳为男,坤地为阴为女 → 天地各正其位而万物生 家庭男女各正其位而家道成 金景芳哲学阐发:这是儒家“天人合一”在家庭领域的体现 3. “家人有严君焉,父母之谓也” “严君”:威严如君的家长 父母并称:突破父权独尊,强调父母共同权威 金景芳引《礼记》:“父亲而母亲”,严慈相济 4. “父父,子子,兄兄,弟弟,夫夫,妇妇”的六伦规范 六组叠字精义: 前一字为名分(父、子、兄、弟、夫、妇) 后一字为责任(行父道、尽子职等) 强调:名实相符,角色与行为一致 与《论语》“君君,臣臣,父父,子子”对照: 孔子对齐景公语侧重政治秩序 此处全面展开家庭六伦,是“齐家”的具体化 5. “正家而天下定矣”的政治哲学结论 逻辑链条:个人修身 → 家庭正伦 → 国家安定 → 天下太平 金景芳历史论证: 周文王“刑于寡妻,至于兄弟,以御于家邦”(《诗经》) 舜处顽父嚣母傲弟之间而家和,终受尧禅 深层思想:家庭是道德训练的第一场所,家风决定国风 四、大象传:“言有物而行有恒”的修身工夫 “风自火出,家人。君子以言有物而行有恒。” 1. 从卦象到修身的转换逻辑 风自火出 → 外在言行源自内在德性 君子观此:确保言行有实质内容且持之以恒 2. “言有物”的三重内涵 不说空话:言必及义,如孔子“不语怪力乱神” 不说假话:修辞立其诚,如《礼记》“不戏谑” 不说废话:言简意赅,如《周易》“吉人之辞寡” 3. “行有恒”的实践要求 家庭场景: 对父母:晨省昏定,持之以恒 对子女:教养有常法,不朝令夕改 金景芳联系《中庸》:“君子之道,造端乎夫妇;及其至也,察乎天地。”家庭中的恒行是成德的起点 五、爻辞精析:家庭各角色的行为规范 家人卦六爻构成一部完整的“家道操作手册”,每爻对应一个家庭角色或情境。 1. 初九:闲有家,悔亡。 “闲”:栅栏,引申为防范、规矩 爻象:初九阳刚居家人之始,如家庭奠基 治家智慧:立规矩宜早不宜迟 “闲有家”:在家庭建立之初就设规立矩 如周公《诫伯禽书》:“我文王之子,武王之弟…然我一沐三捉发,一饭三吐哺” “悔亡”:预先防范则无悔恨 历史例证:颜之推《颜氏家训》早立家规,颜氏一门德业相继 2. 六二:无攸遂,在中馈,贞吉。 全卦主爻之一:女正位乎内的典范 “无攸遂”:不专断,不自作主张 “在中馈”:主持家中饮食起居(引申为内务管理) 爻位:六二柔顺中正,上应九五 儒家女德精义: 非无才能,而是“顺以巽”(柔顺谦逊) 如文母太姒“嗣徽音”,辅助文王治内 金景芳辨析:此爻常被误解为压制女性,实则是强调家庭中合作与分工 3. 九三:家人嗃嗃,悔厉吉;妇子嘻嘻,终吝。 治家刚柔之辨的关键爻 “家人嗃嗃”:严厉训诫声,气氛严肃 表面“悔厉”(令人不安),实则“吉” 如窦燕山《义方训》,五子登科 “妇子嘻嘻”:嬉笑无度,放纵失度 表面和乐,实则“终吝”(终有憾惜) 如《红楼梦》贾府后期家规废弛 爻象:九三阳刚过中,处下卦之极,需以严济宽 治家之道:宁严勿纵,严中有爱 4. 六四:富家,大吉。 “富家”真义:非仅物质富裕,更是德性丰盈 爻位分析: 六四柔顺得正,处上卦巽体(入),善理家财 近九五君位,如贤内助 历史典范: 欧阳修母郑氏“画荻教子”,家贫而德富 孟母三迁,投资于子教,终成亚圣 金景芳阐发:家人卦唯一“大吉”之爻,可见“家富在德不在财” 5. 九五:王假有家,勿恤,吉。 卦主之爻:家长典范 “王假有家”: “假”通“格”,至也 → 王至其家(以身作则) 或释为“王感化其家” 爻象:九五阳刚中正居尊,下应六二 家长之道: “勿恤”:不必忧虑(因治家有方) 关键在“威而有爱,严而能慈” 历史楷模: 汉明帝尊师桓荣,家庭和睦,创明章之治 唐太宗长孙皇后,内助而外不干政 6. 上九:有孚威如,终吉。 “有孚威如”:有诚信而有威严的样子 爻象:上九处家人之终,如家长晚年 治家最高境界: 不怒而威,源于长期积累的信任(孚) 如《礼记》“父子笃,兄弟睦,夫妇和,家之肥也” “终吉”:善始善终,家风永续 历史印证:曾子临终“易箦”,恪守礼制,为家人示范终始如一 六、家人卦的齐家智慧总论 1. 治家三原则: 防闲原则(初九):规矩早立,防微杜渐 正位原则(六二、九五):男女各正其位,分工合作 孚威原则(上九):诚信为本,威严自生 2. 家风建设四要素: 言教:言有物(不说空话假话) 身教:行有恒(以身作则) 严教:嗃嗃吉(适度严格) 德教:富家大吉(以德为富) 3. 与儒家经典的互证: 《大学》:“欲治其国者,先齐其家” 《孝经》:“居家理,故治可移于官” 《孟子》:“天下之本在国,国之本在家” 4. 金景芳总结:家人卦是儒家“亲亲”伦理的易学表达,确立家庭为道德实践的第一场域,其核心是“正”——正位、正伦、正家。
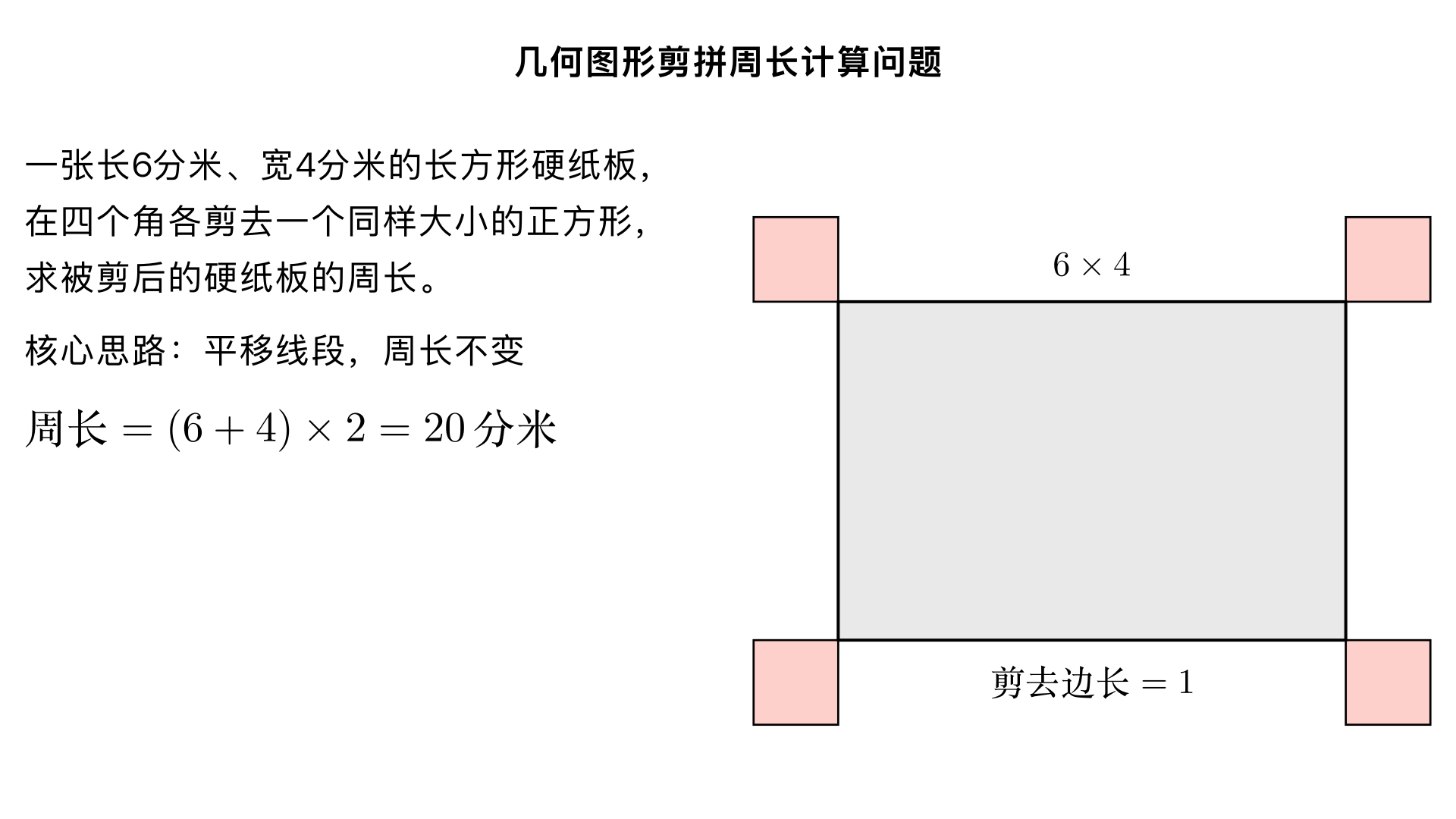
▶
几何图形剪拼周长计算问题:有一张长6分米、宽4分米的长方形硬纸板,在四个角各剪去一个同样大小的正方形,准备做个长方形纸盒。求被剪后的硬纸板的周长? 一、题型判断:几何图形剪拼问题(小学奥数 “长方形剪拼后周长不变” 子类) 这类题型的核心是判断图形剪拼前后的周长变化规律,解题关键是通过平移线段,发现剪去角上的正方形后,周长的总长度没有发生改变,本质是 “平移思想在周长计算中的应用”。 二、解题过程(分 2 步:分析剪拼前后的线段变化→计算周长) 已知条件: 原长方形硬纸板长 6 分米,宽 4 分米; 在四个角各剪去一个同样大小的正方形; 求:剪后硬纸板的周长。 核心逻辑:平移线段,周长不变 我们可以把剪去正方形后,硬纸板边缘凹进去的线段进行平移: 每个角剪去正方形后,会减少正方形的 2 条边,但同时会增加正方形另外 2 条等长的边; 把凹进去的水平线段向上 / 向下平移,竖直线段向左 / 向右平移,最终可以拼成和原来长方形完全一样的轮廓。 简单说:剪去四个角的正方形,没有改变硬纸板的周长总长度。 步骤:计算原长方形的周长 长方形周长公式:周长 = (长 + 宽)× 2代入数据:周长 = (6 + 4)× 2 = 10 × 2 = 20 分米 三、反推验证(核对线段长度,确认周长不变) 假设剪去的正方形边长为 1 分米: 原长方形周长:(6+4)×2=20 分米; 剪后硬纸板的水平线段总长度:(6 - 1 - 1) + 1 + 1 + (6 - 1 - 1) + 1 + 1 = 6 + 6 = 12 分米; 剪后硬纸板的竖直线段总长度:(4 - 1 - 1) + 1 + 1 + (4 - 1 - 1) + 1 + 1 = 4 + 4 = 8 分米; 剪后总周长:12 + 8 = 20 分米,和原长方形周长一致 ✔️; 再假设正方形边长为 2 分米(最大可剪的正方形,边长不超过宽的一半): 剪后水平线段总长:(6-2-2)+2+2+(6-2-2)+2+2=6+6=12 分米; 剪后竖直线段总长:(4-2-2)+2+2+(4-2-2)+2+2=4+4=8 分米; 总周长:12+8=20 分米,依然和原周长一致 ✔️; 逻辑验证:无论剪去的正方形边长是多少,平移后线段总长度都等于原长方形的长和宽之和的 2 倍,周长不变 ✔️。 四、最终结果 被剪后的硬纸板的周长是 20 分米。
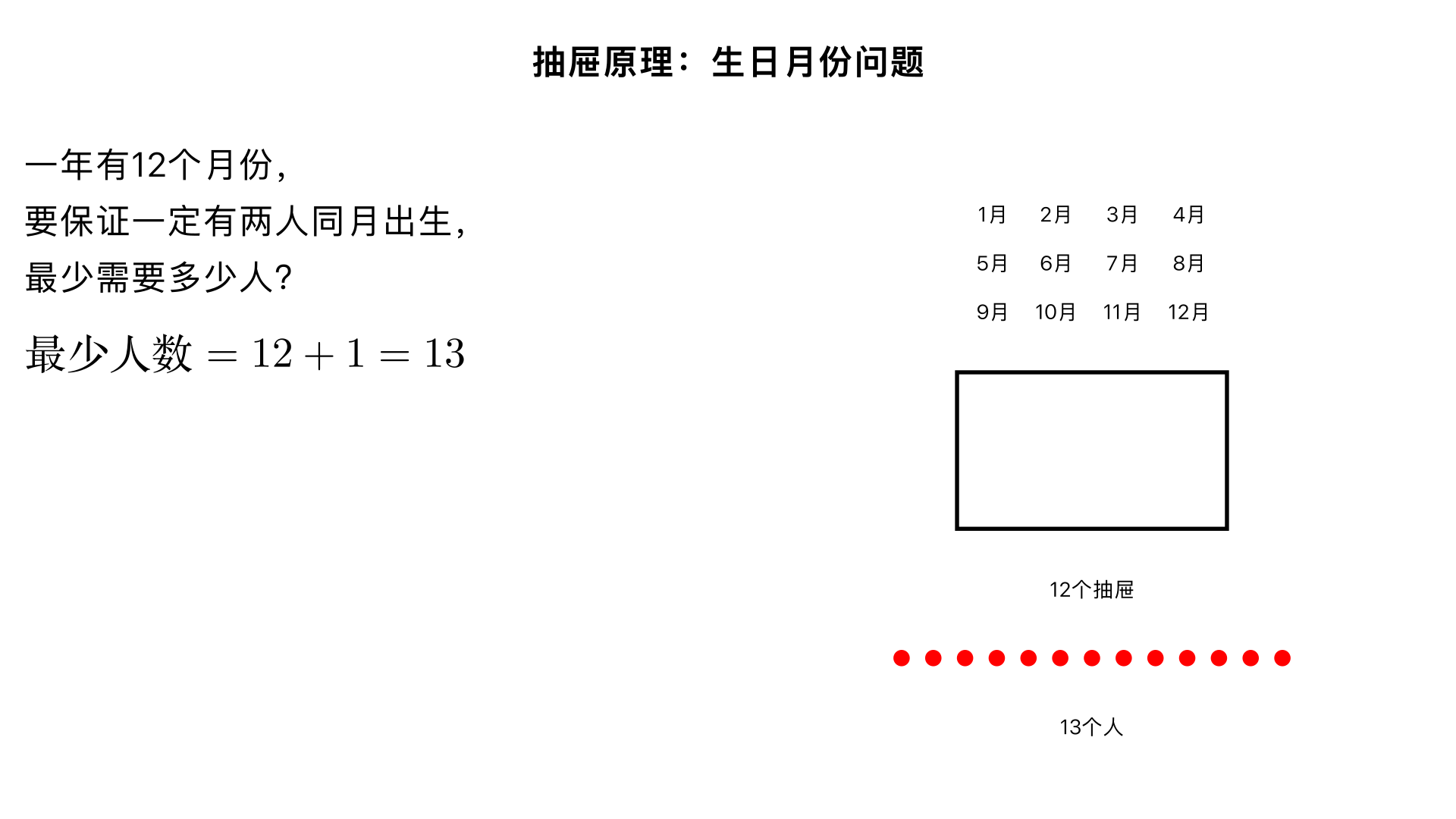
▶
至少在多少个人中,一定能找到两个同一月份出生的人? 一、题型判断:抽屉原理问题(小学奥数 “抽屉原理之最不利原则” 子类) 这类题型的核心是把 “月份” 当作 “抽屉”,“人” 当作 “物品”,通过考虑最不利的分配情况,计算保证出现重复抽屉的最少物品数量。解题关键是先确定抽屉的数量,再利用 “抽屉数 + 1” 的规律得出结论,本质是极端假设思想的应用。 二、解题过程(分 3 步:确定抽屉数→分析最不利情况→计算最少人数) 已知条件: 一年有 12 个不同的月份(即 “抽屉” 数量为 12); 目标:保证一定能找到两个同一月份出生的人。 核心逻辑:要 “保证” 有两人同月出生,先考虑最不利的情况 —— 让每个人的出生月份都不同,当把所有月份都占满后,再多 1 个人,这个人的出生月份必然和前面某个人重复。 步骤 1:确定抽屉数量 一年有 12 个月份,所以 “抽屉数”=12。 步骤 2:分析最不利情况 最不利的情况:前 12 个人的出生月份完全不同,刚好每个月份都有 1 个人(相当于 12 个抽屉各放 1 个物品),此时没有任何两个人是同月出生的。 步骤 3:计算最少人数 在最不利情况的基础上,再增加 1 个人,这个人的出生月份一定是 12 个月份中的某一个,就必然会和前面 12 人中的某个人同月出生。因此,最少人数 = 抽屉数 + 1 = 12 + 1 = 13 人。 三、反推验证(核对逻辑合理性,确认结果无误) 最不利情况验证:12 个人时,存在 “每人出生月份都不同” 的可能性(1 月到 12 月各 1 人),此时无法保证有两人同月出生 ✔️; 必然性验证:当有 13 个人时,即使前 12 个人分属不同月份,第 13 个人的出生月份必然属于 12 个月份中的某一个,就一定会和前面某个人同月出生,满足 “保证” 的条件 ✔️; 逻辑闭环验证:抽屉数(12 个月份)+1=13 人,计算过程无误差,完全符合抽屉原理的核心规律 ✔️。 四、最终结果 至少在 13 个人 中,一定能找到两个同一月份出生的人。

▶
抽屉中有2颗红珠子、4颗蓝珠子、6颗绿珠子,如果闭上眼睛摸一摸,必须摸几颗珠子才能保证至少有1颗绿珠子? 一、题型判断:抽屉原理问题(小学奥数 “抽屉原理之最不利原则” 子类) 这类题型的核心是通过 “考虑最不利的极端情况”,计算保证摸到目标物品的最少次数。解题关键是先摸完所有 “非目标物品”,再摸 1 个就必然是目标物品,本质是 “极端假设思想在抽屉原理中的基础应用”,核心是 “不抱侥幸,先算最坏情况”。 二、解题过程(分 3 步:找非目标物品→算最不利次数→求最少摸取数) 已知条件: 抽屉中有红珠子 2 颗、蓝珠子 4 颗、绿珠子 6 颗(目标:绿珠子;非目标:红、蓝珠子); 要求:保证至少摸到 1 颗绿珠子,求最少摸取的珠子数量。 核心逻辑:要 “保证” 摸到绿珠子,必须先考虑 “最倒霉” 的情况 —— 把所有不是绿珠子的都摸完,此时再摸 1 颗,一定是绿珠子。 步骤 1:计算非目标珠子的总数量 非目标珠子(红 + 蓝)的总数 = 红珠子数量 + 蓝珠子数量= 2 + 4 = 6 颗。 步骤 2:分析最不利情况的摸取次数 最不利情况:先把 6 颗非目标珠子(2 红 + 4 蓝)全部摸出,此时手里有 6 颗珠子,但没有 1 颗绿珠子(这是 “最多摸不到绿珠子” 的极限数量)。 步骤 3:计算保证摸到绿珠子的最少次数 在最不利情况的基础上,再摸 1 颗珠子,无论这颗是什么颜色,都只能是绿珠子(非目标珠子已摸完)。因此,最少摸取次数 = 非目标珠子总数 + 1 = 6 + 1 = 7 颗。 三、反推验证(核对逻辑,确认结果无误差) 最不利情况验证:摸 6 颗珠子时,有可能是 2 红 + 4 蓝(无绿珠子),这是 “最倒霉” 的极限,确实摸不到绿珠子 ✔️; 必然性验证:摸第 7 颗珠子时,抽屉里剩下的只有绿珠子(6 颗),所以第 7 颗一定是绿珠子,此时手里至少有 1 颗绿珠子,完全满足 “保证” 的要求 ✔️; 反向验证:若只摸 6 颗,无法保证有绿珠子(可能全是红、蓝);若摸 7 颗,无论如何都必有绿珠子,说明 7 颗是 “最少能保证” 的数量 ✔️; 数量计算验证:2+4=6(非目标总数),6+1=7,计算无错误,逻辑闭环 ✔️。 四、最终结果 必须摸 7 颗 珠子才能保证至少有 1 颗绿珠子。
▶