T
Teach Me AnythingTMA
Video History
Page 10 / 126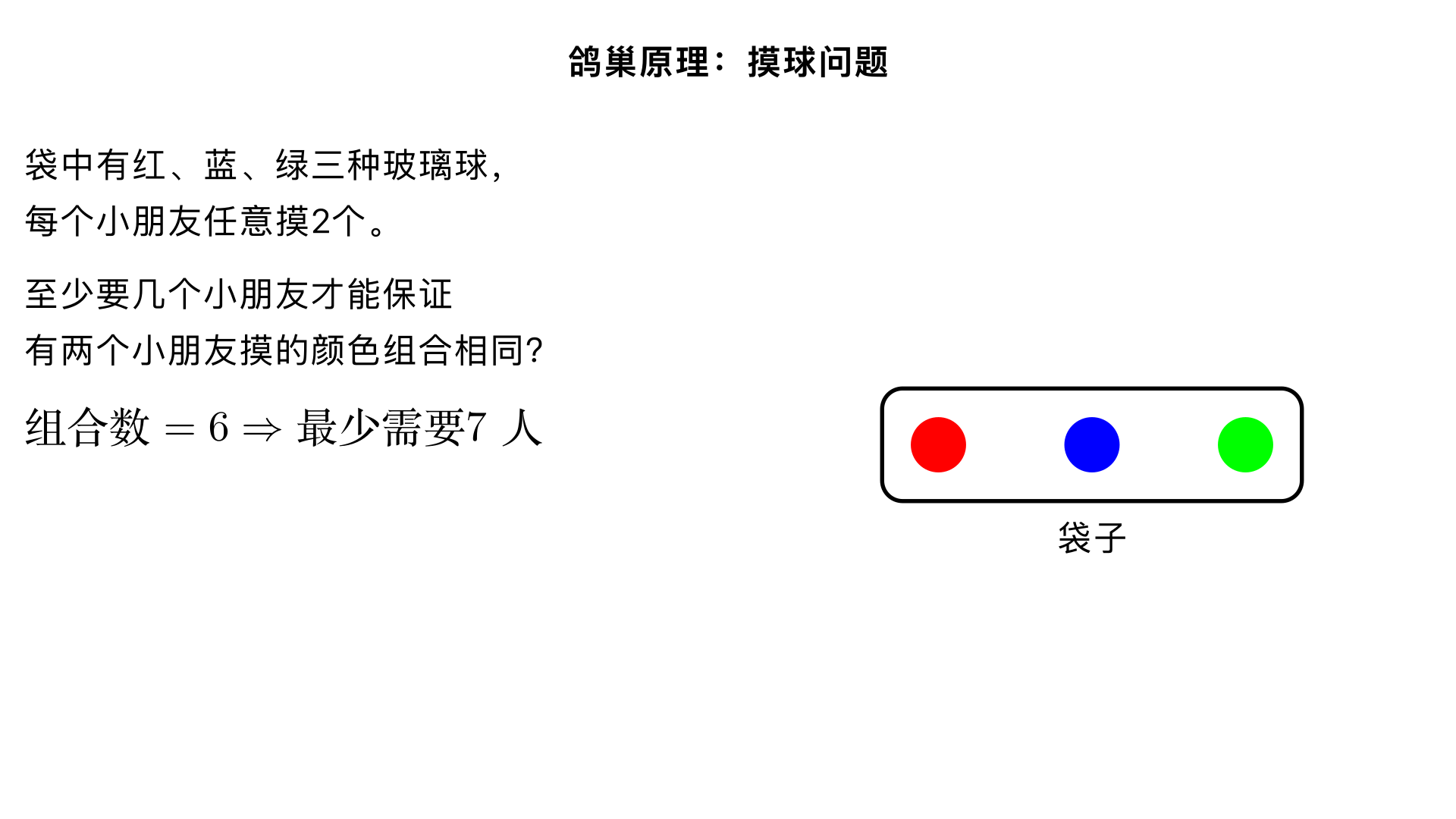
▶
鸽巢原理:袋子中有红、蓝、绿三种玻璃球,每个小朋友任意摸2个玻璃球,那至少要几个小朋友才能保证有两个或两个以上的小朋友所摸的玻璃球的颜色相同? 一、题型判断:鸽巢原理问题(小学奥数“鸽巢原理基础应用”子类) 这类题型的核心是“找出所有可能的结果(鸽巢),再根据‘保证有重复结果’的要求,计算最少的尝试次数(鸽子数量)”。解题关键是先枚举所有不重复的情况(确定鸽巢数量),再利用“鸽巢数+1”的规律得出结论,本质是“最不利原则与鸽巢分类的结合应用”——即先考虑最倒霉的情况(所有小朋友摸的球颜色组合都不同),在此基础上再增加1人,就能保证有重复。 二、解题过程(分3步:枚举摸球组合→确定鸽巢数量→计算最少人数) 已知条件: •袋子中有红、蓝、绿三种颜色的玻璃球; •每个小朋友任意摸2个玻璃球; •目标:保证有两个或两个以上小朋友摸的玻璃球颜色相同,求最少需要的小朋友人数。 核心逻辑:先找出“摸2个玻璃球”的所有不同颜色组合(这是“鸽巢”),再根据最不利原则,先让每个小朋友摸的组合都不同(每个鸽巢先放1只鸽子),再增加1个小朋友,就必然会出现重复组合。 步骤1:枚举所有不同的摸球颜色组合 摸2个玻璃球的情况分为两类:“两个球颜色相同”和“两个球颜色不同”,逐一列举: •颜色相同的组合:① 2个红色;② 2个蓝色;③ 2个绿色;共3种; •颜色不同的组合:④ 1个红色+1个蓝色;⑤ 1个红色+1个绿色;⑥ 1个蓝色+1个绿色;共3种; 综上,所有不同的摸球组合一共有:3+3=6种(即鸽巢数量为6)。 步骤2:根据最不利原则计算最少小朋友人数 最不利的情况:前6个小朋友摸的玻璃球颜色组合完全不同,刚好每个组合对应1个小朋友(6个鸽巢各放1只鸽子); 此时,只要再增加1个小朋友(第7个),无论他摸的是哪一种组合,都会和前面6个小朋友中的某一个组合重复,就能保证有两个或两个以上小朋友摸的颜色组合相同。 因此,最少需要的小朋友人数=6+1=7人。 三、反推验证(核对逻辑合理性,确认结果无误) •组合完整性验证:摸2个球的所有可能组合已全部枚举(3种同色+3种异色),共6种,无遗漏、无重复 ✔️; •最不利情况验证:前6个小朋友分别对应6种不同组合(如小朋友1摸2红、小朋友2摸2蓝、小朋友3摸2绿、小朋友4摸红蓝、小朋友5摸红绿、小朋友6摸蓝绿),此时确实没有任何两个小朋友组合相同,符合“最倒霉”的假设 ✔️; 1.结果验证:第7个小朋友无论摸哪种组合(比如摸2红),都会和小朋友1的组合重复,因此必然满足“有两个或两个以上小朋友摸的颜色相同”的条件 ✔️; ○反向验证:若只有6个小朋友,存在“所有组合都不同”的可能,无法保证重复,因此6人不符合要求,进一步说明7人是最少人数 ✔️。 四、最终结果 至少要7个小朋友才能保证有两个或两个以上的小朋友所摸的玻璃球的颜色相同。
▶
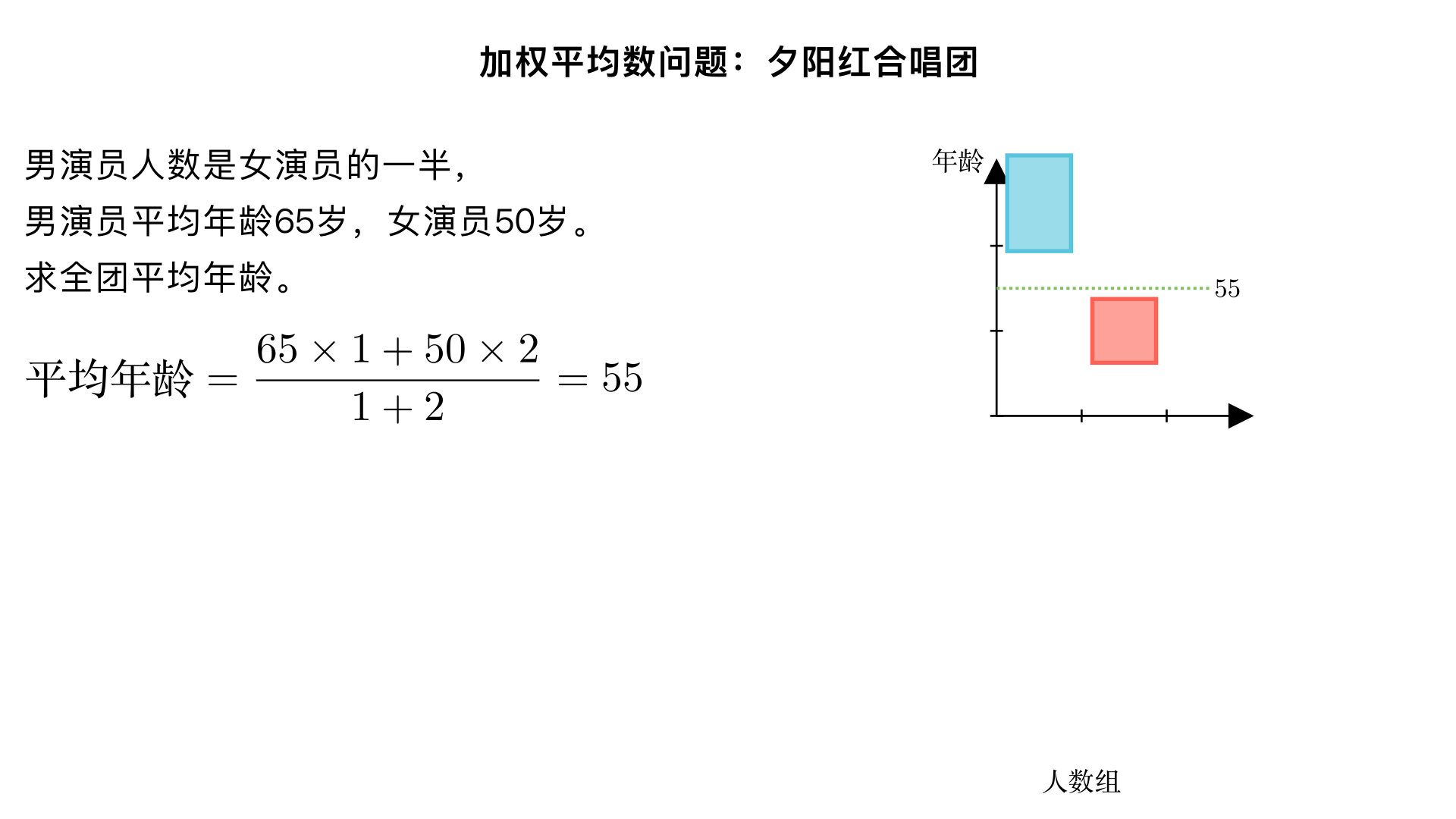
权平均数问题:“夕阳红合唱团男演员的人数是女演员人数的一半.男演员的平均年龄是65岁,女演员的平均年龄是50岁。全团演员的平均年龄是多少岁? 一、题型判断:平均数问题(小学奥数“加权平均数”子类) 这类题型的核心是考虑不同数量的群体对整体平均数的影响,需要用“各群体的总数量(总年龄)之和 ÷ 总份数(总人数)”计算加权平均数,解题关键是通过设数法确定男、女演员的人数,再计算总年龄和总人数,本质是“加权思想在平均数计算中的应用”。 二、解题过程(分3步:设数定人数→计算总年龄→求加权平均数) 已知条件: •男演员人数 = 12 × 女演员人数; •男演员平均年龄 = 65岁,女演员平均年龄 = 50岁; 核心逻辑:因为男、女演员人数是比例关系,可设具体人数简化计算(设女演员人数为2份,男演员为1份,方便计算)。 步骤1:设定男、女演员的人数 为了计算方便,设男演员有1人,根据“男演员人数是女演员的一半”,则女演员有2人。 (也可以设男演员为x人,女演员为2x人,最终x会被约掉,结果一致) 步骤2:计算男、女演员的总年龄 •男演员总年龄 = 人数 × 平均年龄 = 1×65=65 岁; •女演员总年龄 = 人数 × 平均年龄 = 2×50=100 岁; •全团总年龄 = 男演员总年龄 + 女演员总年龄 = 65+100=165 岁。 步骤3:计算全团总人数和平均年龄 •全团总人数 = 男演员人数 + 女演员人数 = 1+2=3 人; •全团平均年龄 = 全团总年龄 ÷ 全团总人数 = 165÷3=55 岁。 三、反推验证(换人数假设,确认结果一致) 1.验证设数合理性:假设男演员有10人,女演员则有20人 ○男演员总年龄 = 10×65=650 岁; ○女演员总年龄 = 20×50=1000 岁; ○全团总年龄 = 650+1000=1650 岁; ○全团总人数 = 10+20=30 人; ○全团平均年龄 = 1650÷30=55 岁,与之前结果一致 ✔️。 2.公式验证(代数法):设男演员x人,女演员2x人 ○全团平均年龄 = 65x+50×2xx+2x=65x+100x3x=165x3x=55 岁,x约掉后结果不变 ✔️。 四、最终结果 全团演员的平均年龄是 55岁。
▶
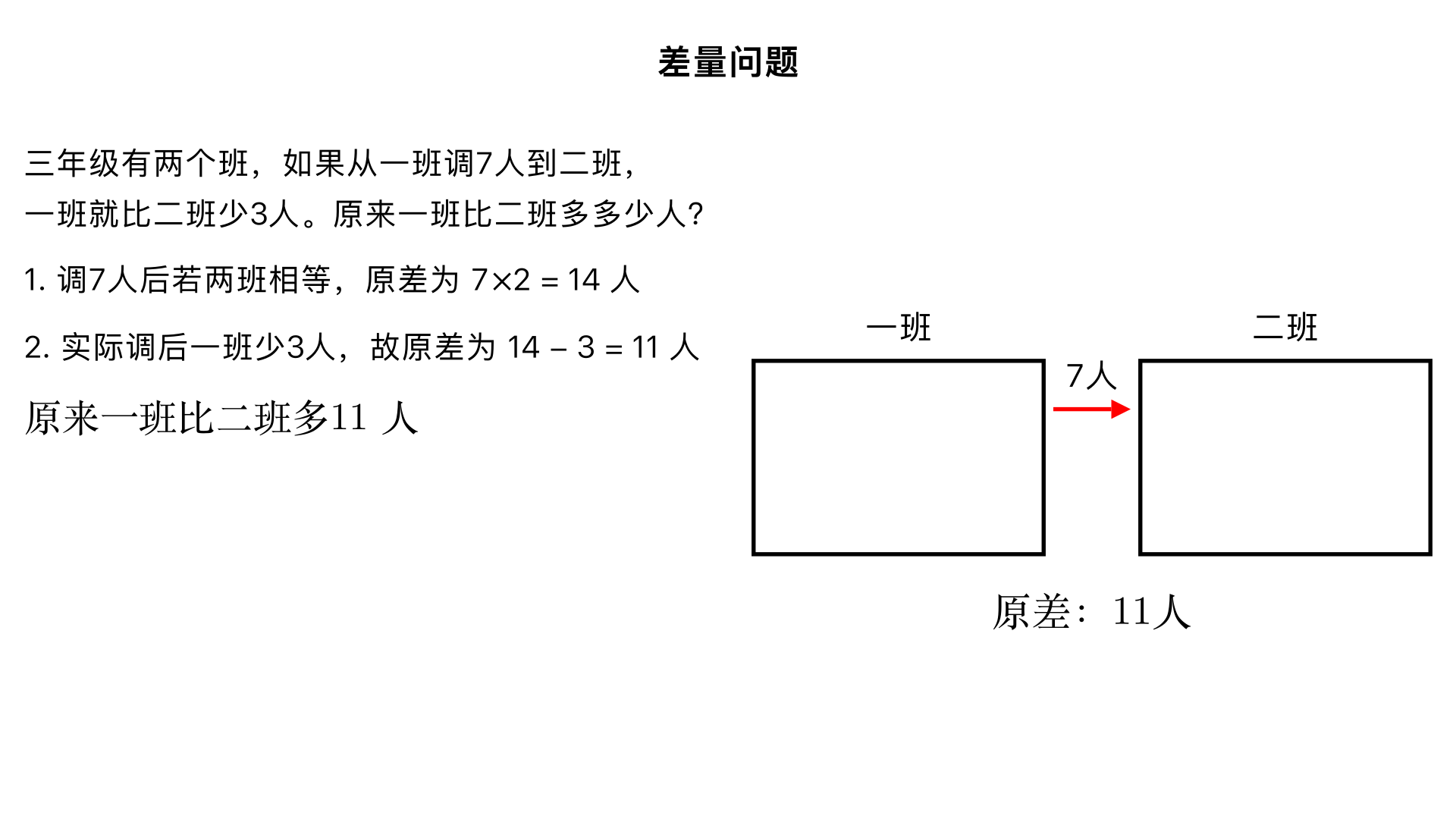
差量问题-三年级有两个班,如果从一班调7人到二班去,一班就比二班少3人。原来一班比二班多多少人? 一、题型判断:和差问题延伸(小学奥数 “移多补少型差量问题” 子类) 这类题型的核心是抓住 “人员调动前后的数量差变化规律”,理解 “调走人数” 和 “最终差值” 之间的关系,解题关键是明确 “移动的人数 ×2” 与 “原来的差值”“最终的差值” 的关联,本质是 “数量差在移多补少场景下的应用”。 二、解题过程(分 2 步:分析调动后的差值变化→计算原来的人数差) 已知条件: 从一班调 7 人到二班; 调动后,一班比二班少 3 人;核心逻辑:如果从一班调 7 人到二班后,两班人数相等,说明一班原来比二班多 \(7×2=14\) 人;但现在调动后一班反而少 3 人,说明原来的差值要比 14 人少 3 人。 步骤 1:分析 “无差值” 时的原差量 若调 7 人后两班人数相等,意味着一班减少 7 人、二班增加 7 人后人数相同,此时一班原来比二班多:\(7+7=14\) 人 步骤 2:结合最终差值计算原差量 现在调 7 人后,一班比二班少 3 人,说明一班原来的人数差没有达到 14 人,需要减去这个 “少的 3 人”:原来一班比二班多的人数 = \(14-3=11\) 人 三、反推验证(模拟调动过程,确认差值一致) 假设原来一班有 x 人,二班有 y 人,根据计算结果,\(x-y=11\),即 \(x=y+11\); 从一班调 7 人到二班后: 一班人数变为 \(x-7 = y+11-7 = y+4\); 二班人数变为 \(y+7\); 此时一班比二班少的人数:\((y+7)-(y+4)=3\) 人,与题目条件完全一致 ✔️; 总数验证:调动前后两班总人数不变(\(x+y=(x-7)+(y+7)\)),逻辑自洽 ✔️。 四、最终结果 原来一班比二班多 11 人。

▶
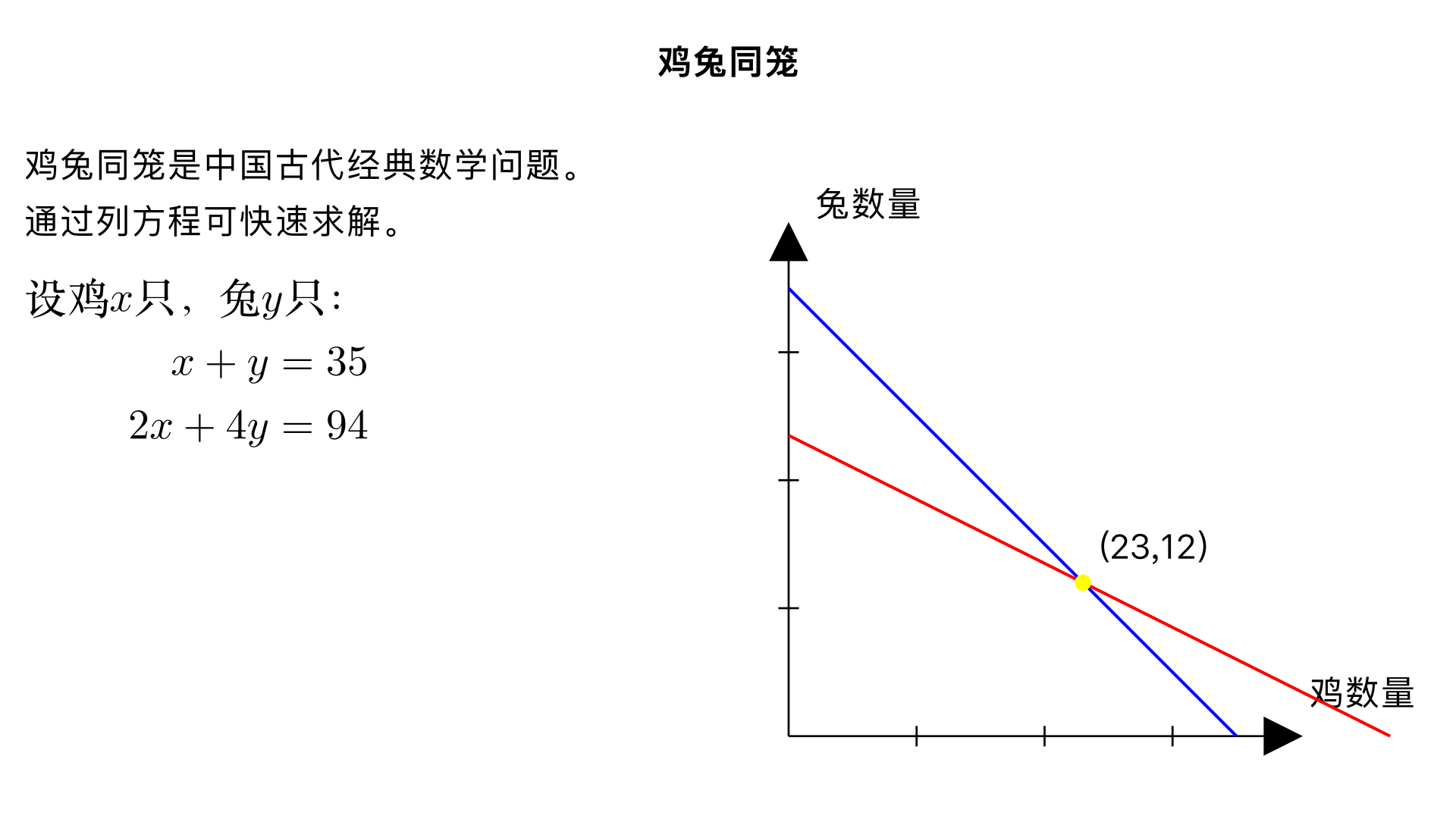
鸡兔同笼问题:每个大油桶可装油6千克,每个小油桶可装油2千克,大油桶和小油桶共50个,大油桶比小油桶共多装油60千克。大、小油桶各有多少个? 一、题型判断:鸡兔同笼问题(小学奥数 “鸡兔同笼变例 —— 和差型” 子类) 这类题型是鸡兔同笼的经典变形,核心是通过 “两种容器的总数” 和 “两种容器装油量的差值”,替代传统鸡兔同笼的 “总头数” 和 “总脚数”,解题关键是利用假设法,结合数量差与装油量差建立等式,本质是 “假设思想在差值问题中的应用”。 二、解题过程(分 4 步:假设全为大油桶→计算差值偏差→调整数量→求出结果) 已知条件: 大、小油桶总数 = 50 个; 每个大桶可装 6 千克,每个小桶可装 2 千克; 大油桶装油总量 - 小油桶装油总量 = 60 千克;核心逻辑:假设全部是大油桶,计算此时的装油差值,与实际差值对比,通过每替换一个桶的差值变化,求出小油桶数量。 步骤 1:假设 50 个全是大油桶 此时小油桶数量 = 0,大油桶装油总量 = 50×6=300 千克,小油桶装油总量 = 0×2=0 千克,假设的差值=300 - 0=300 千克。 步骤 2:计算假设差值与实际差值的偏差 实际差值 = 60 千克,偏差值 = 假设差值 - 实际差值 = 300 - 60=240 千克。偏差原因:把小油桶当成大油桶,不仅大桶数量多算、小桶数量少算,还导致装油的差值被大幅高估。 步骤 3:分析每替换 1 个桶的差值变化 每把 1 个大油桶换成小油桶,大桶数量减 1,小桶数量加 1: 大桶装油总量减少 6 千克; 小桶装油总量增加 2 千克;因此,大桶与小桶的装油差值会减少 6+2=8 千克(大的少 6,小的多 2,一减一加,差值共减少 8)。 步骤 4:计算小油桶数量和大油桶数量 需要替换的次数 = 偏差值 ÷ 每次替换的差值减少量 = 240÷8=30 次,即小油桶数量 = 30 个,大油桶数量 = 总数 - 小油桶数量 = 50 - 30=20 个。 三、反推验证(核对装油量差值,确认一致) 计算大、小油桶的装油总量: 大油桶装油 = 20×6=120 千克; 小油桶装油 = 30×2=60 千克; 验证装油量差值:120 - 60=60 千克,与题目条件一致 ✔️; 验证总数:20 + 30=50 个,与题目总数一致 ✔️; 逻辑验证:每替换 1 个桶差值减少 8 千克,30 次替换减少 240 千克,300 - 240=60 千克,完全符合实际差值 ✔️。 四、最终结果 大油桶有 20 个,小油桶有 30 个。
▶
鸡兔同笼
▶
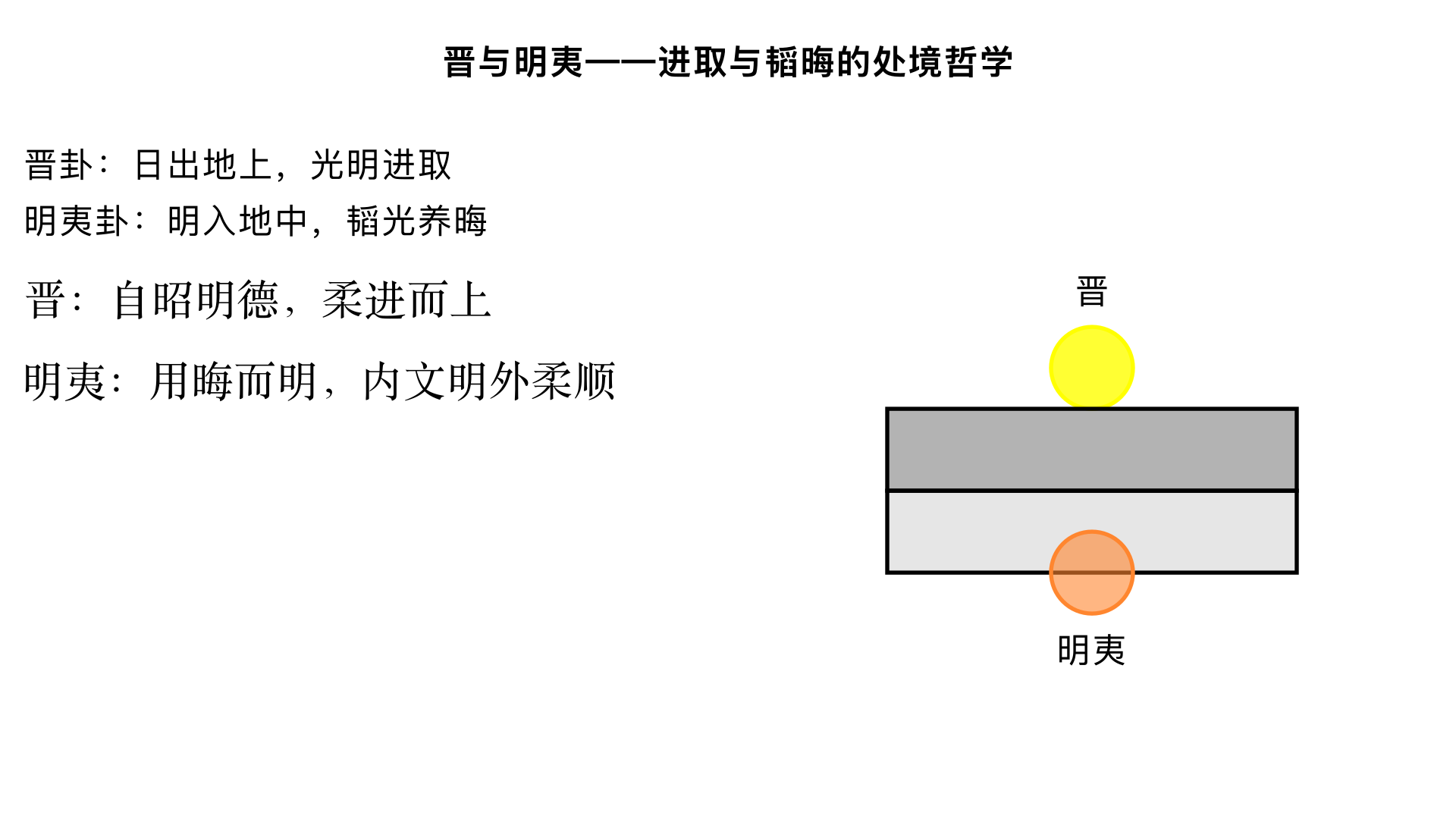
晋与明夷——进取与韬晦的处境哲学 一、晋卦(火地晋)——进取晋升之道 1. 卦序的逻辑推进 大壮是强盛,但强盛之后需有方向,《序卦传》:“物不可以终壮,故受之以晋。晋者,进也。” 晋卦揭示:真正的强大不是停滞,而是光明正大地前进。 2. 卦象的文明意蕴 基本卦象:上离火,下坤地 → 日出地上,光明普照 卦德结构:坤顺离明 → 柔顺而附丽于光明 文化象征:太阳升起,文明进步,人才晋升 金景芳阐发:晋卦是《周易》中最具“文明进步”色彩的卦,反映周代“郁郁乎文哉”的精神。 3. 《彖传》的晋升哲学 text 晋,进也。明出地上。 顺而丽乎大明,柔进而上行。 是以康侯用锡马蕃庶,昼日三接也。 “明出地上”:双重含义 自然现象:太阳从地平线升起 人文精神:光明德性彰显于世 “顺而丽乎大明”: 下坤为顺,上离为大明 → 以柔顺之德依附光明(君德或大道) 金景芳释:此句揭示儒家晋升的核心——不是靠钻营,而是“以德配位” “柔进而上行”: 指六五阴爻居尊位,以柔德晋升 打破“阳尊阴卑”的刻板印象,强调柔德也能上升 “康侯用锡马蕃庶”典故: 康侯:卫康叔,周武王之弟,治卫有方 “锡马蕃庶”:受赐众多车马(物质奖励) “昼日三接”:一日内多次接见(荣誉肯定) 金景芳考证:此反映周初“明德慎罚”的治国理念,有功者必赏 4. 《大象传》的德性修养 “明出地上,晋。君子以自昭明德” “自昭明德”四字精义: 自:主体自觉,非外力逼迫 昭:彰显、发扬,非隐藏 明德:光明的德性(《大学》“明明德”) 修养次第:如太阳升起,由暗而明,由微而著 金景芳联系《大学》:格物→致知→诚意→正心→修身→齐家→治国→平天下,正是“自昭明德”的过程 5. 爻辞的晋升阶梯 晋卦六爻描绘了从基层到高位的完整晋升之路,每爻都有其境遇和智慧。 初六:晋如摧如,贞吉。罔孚,裕无咎。 “晋如摧如”:前进与受阻交替 初爻困境:位卑力弱,不被信任(“罔孚”) 破解之道:“裕无咎”——宽裕从容,不急躁 爻象:初六阴爻居下,与九四相应但距离远 历史类比:姜子牙渭水垂钓,待时而动 六二:晋如愁如,贞吉。受兹介福,于其王母。 “愁如”心理:前进中充满忧虑 爻位优势:六二柔中得正,虽无应(与六五同阴),但同德 “王母”象征:六五阴爻为“王母”(祖母辈),象征慈祥的上司 “介福”:大福,来自德性感应而非钻营 现实意义:扎实工作终获赏识,如百里奚被秦穆公发现 六三:众允,悔亡。 简单爻辞,深意存焉:六三不中不正,本应有悔 “众允”力量:得到众人信任支持 爻象:处坤卦之极,顺德至诚,故得众心 金景芳点题:晋升需群众基础,德性比位置更重要 历史印证:舜“耕历山,历山之人皆让畔”,众允故受尧禅 九四:晋如鼫鼠,贞厉。 “鼫鼠”比喻:五技鼠(能飞不能过屋,能缘不能穷木,能游不能渡谷,能穴不能掩身,能走不能先人) 象征:贪居高位而无真才实德 爻象:九四阳居阴位,不中不正,处近君之位而德不配 “贞厉”警示:即使动机纯正也危险 历史典型:赵括纸上谈兵,终致长平之败 六五:悔亡,失得勿恤,往吉无不利。 卦主之爻:六五阴居尊位,为晋卦主爻 “悔亡”条件:虽以阴居阳,但有柔中之德 “失得勿恤”境界:超越得失计较 爻象精微:下有三阴爻顺承,上有上九相佐 君主典范:汉文帝轻徭薄赋,不患得失,开创文景之治 上九:晋其角,维用伐邑,厉吉无咎,贞吝。 “晋其角”:晋升到顶点(角为顶端) “维用伐邑”:只能用于讨伐自己的属邑(内部治理) 爻象:上九处晋之极,进无可进 “厉吉无咎”辩证:看似危险(厉),实则吉而无咎 “贞吝”提醒:若不知止而欲外扩,则吝 历史教训:汉武帝晚年轮台罪己,由外征转为内治 6. 晋卦的晋升智慧总结 晋升三要素: 德性基础:自昭明德 群众支持:众允悔亡 时机把握:失得勿恤 晋升三禁忌: 急躁冒进:晋如摧如 德不配位:晋如鼫鼠 不知止进:晋其角 金景芳总论:晋卦是儒家“学而优则仕”的易学表达,但强调“仕”必须以“德”为本。 二、明夷卦(地火明夷)——韬晦保全之道 1. 卦序的深刻转折 《序卦传》:“晋者,进也。进必有所伤,故受之以明夷。夷者,伤也。” 光明晋升(晋)之后可能受到伤害,揭示“福兮祸所伏”的辩证规律。 晋卦(䷢)与明夷卦(䷣)互为覆卦(综卦),象征光明与黑暗的转换。 2. 卦象的黑暗境遇 基本卦象:上坤地,下离火 → 明入地中,光明被掩 卦德结构:坤顺离明 → 内怀文明之德,外示柔顺之态 时代象征:黑暗时期,贤者受压抑 金景芳历史定位:明夷卦是《周易》中最具历史悲剧感的卦,反映商周之际的黑暗时代。 3. 《彖传》的历史哲学 text 明入地中,明夷。 内文明而外柔顺,以蒙大难,文王以之。 利艰贞,晦其明也,内难而能正其志,箕子以之。 “明入地中”:光明沉入地下,黑暗笼罩 “内文明而外柔顺”: 下离为内文明,上坤为外柔顺 这是明夷卦的核心处世智慧 “以蒙大难,文王以之”: 文王典范:被囚羑里七年,演《周易》,内怀文明(推演天道),外示柔顺(臣服纣王) 金景芳考证:文王“三分天下有其二,以服事殷”,是“外柔顺”的极致 “晦其明也”:隐藏光明,韬光养晦 “内难而能正其志,箕子以之”: 内难:内部灾难(箕子是纣王叔父,亲人残暴) 正其志:端正心志,不随波逐流 箕子选择:伴狂为奴,后出走朝鲜,传道东方 金景芳阐发:明夷卦提供了两种处世模式——文王式(等待时机)和箕子式(保全文化),都是儒家认可的“权变”。 4. 《大象传》的政治智慧 “明入地中,明夷。君子以莅众,用晦而明” “用晦而明”四字精义: 表面用晦:不察察为明,不显示小聪明 实质求明:把握大方向,大智若愚 政治应用: 对民众:不苛察细过(如曹参“萧规曹随”) 对下属:不事必躬亲(如汉高祖用三杰) 金景芳联系黄老思想:与老子“其政闷闷,其民淳淳”相通,但儒家“用晦”是为“明”,目的不同 5. 爻辞的黑暗生存术 明夷卦六爻几乎都可找到历史人物对应,构成一部“黑暗时代生存指南”。 初九:明夷于飞,垂其翼。君子于行,三日不食。有攸往,主人有言。 “明夷于飞”象征:光明受伤时飞翔(逃离) “垂其翼”:垂下翅膀,低调飞行 “三日不食”:急速逃离,不及饮食 爻象:初九阳刚处明夷之初,见几最早 人物对应:微子见纣不可谏,抱祭器投周 金景芳赞:“识时务者为俊杰”,初九是明夷中的智者 六二:明夷,夷于左股,用拯马壮,吉。 “夷于左股”:左腿受伤(左为阳,象征轻微伤) “用拯马壮”:用壮马来拯救 爻象:六二柔中得正,受伤但得救 象征意义:在黑暗时期受轻伤,但得有力援助 历史类比:胶鬲被纣王迫害,得文王拯救 九三:明夷于南狩,得其大首,不可疾贞。 “南狩”:向南征伐(周在商之西,向南指伐纣) “得其大首”:获得元凶(纣王) 爻象:九三阳刚得位,处离明之极 “不可疾贞”:不可急于求正,需等待时机 历史印证:武王观兵孟津,诸侯皆曰“纣可伐”,武王曰“未可”,待时机成熟 金景芳阐发:九三揭示革命之道——光明力量需积蓄待发 六四:入于左腹,获明夷之心,于出门庭。 “入于左腹”:进入左腹(深入内部了解) “获明夷之心”:了解黑暗的根源 “于出门庭”:于是出门远走 爻象:六四柔位,处坤卦下爻,近黑暗中心 人物对应:箕子身为纣王叔父,深知其恶,伴狂后出走 金景芳解析:此爻揭示“知黑守白”的智慧 六五:箕子之明夷,利贞。 直接以箕子命名:极为罕见,显示此爻的特殊性 “箕子之明夷”:箕子式的光明伤损 “利贞”:利于守正 爻象:六五居尊位但阴柔,处黑暗中心 行为选择:伴狂为奴,保全文化,等待复兴 金景芳评价:箕子选择比干(死谏)、微子(逃离)更艰难,但也更伟大 上六:不明晦,初登于天,后入于地。 “不明晦”:不明反而晦暗(以黑暗为光明) “初登于天”:开始升到天上(纣王初登王位) “后入于地”:后来坠入地下(自焚鹿台) 爻象:上六处明夷之极,黑暗到极点 天道循环:黑暗终将灭亡,光明终将复来 金景芳总结:此爻是《周易》的历史审判,宣告“多行不义必自毙” 6. 明夷卦的韬晦智慧总结 三个历史典范: 文王模式:内文明外柔顺,等待时机 箕子模式:晦其明而正其志,文化传承 微子模式:明夷于飞,适时逃离 黑暗生存四原则: 见几而作(初九):察觉危险及时行动 用拯马壮(六二):寻求外部援助 不可疾贞(九三):不急躁,待时而动 利贞守志(六五):坚守正道不妥协 金景芳哲学升华:明夷卦揭示“黑暗是光明的考验”,真正的光明能在黑暗中不灭,如文王拘而演《易》,孔子困而作《春秋》,司马迁辱而著《史记》。 三、晋与明夷的辩证关系 1. 光明与黑暗的循环 text 晋卦(䷢):明出地上 → 光明时代,积极进取 明夷卦(䷣):明入地中 → 黑暗时代,韬光养晦 二卦构成一对矛盾,反映历史治乱循环 金景芳指出:这正是《诗经》“高岸为谷,深谷为陵”的易学表达 2. 君子之道的完整性 顺境之道(晋卦):自昭明德,柔进而上 逆境之道(明夷卦):用晦而明,内文明外柔顺 共同核心:无论顺逆,保持内心光明(离明之德) 3. 历史哲学的深度 晋卦可对应西周成康之治 明夷卦可对应商周革命之际 金景芳总结:二卦连读,可理解中国历史上“一治一乱”的深层规律 四、四卦(遁、大壮、晋、明夷)的综合哲学 1. 完整的处境应对体系 卦名 时势特征 核心智慧 关键爻辞 历史人物 遁卦 小人道长 适时而退 肥遁无不利 范蠡、张良 大壮 阳气强盛 非礼弗履 小人用壮君子用罔 汉武帝、唐太宗 晋卦 光明上升 自昭明德 受兹介福于其王母 卫康叔、诸葛亮 明夷 黑暗笼罩 用晦而明 内文明外柔顺 文王、箕子 2. “时”与“位”的极致运用 遁卦:“与时行也”(时) 大壮:“刚以动”(位) 晋卦:“柔进而上行”(时位结合) 明夷:“内难而能正其志”(位中守时) 金景芳强调:四卦共同体现《周易》“时中”哲学——根据时势和位置采取最恰当行动。 3. 儒家处世哲学的易学表达 穷达之辨的完整回答: 达时(晋、大壮):如何进取而不失正道 穷时(遁、明夷):如何退守而不失志节 与《孟子》对照: “穷则独善其身” → 遁卦、明夷卦 “达则兼济天下” → 晋卦、大壮卦 4. 现代启示 个人层面:在职场、人生不同阶段,如何进退有据 组织层面:企业盛衰周期中的战略调整 国家层面:文明兴衰中的文化坚守与创新 5. 学习要点 背诵四卦的《彖传》,理解各自的核心思想 掌握每卦的关键爻辞及历史典故 思考:在当代社会,如何创造性地运用这些智慧?

▶
什么是电
▶
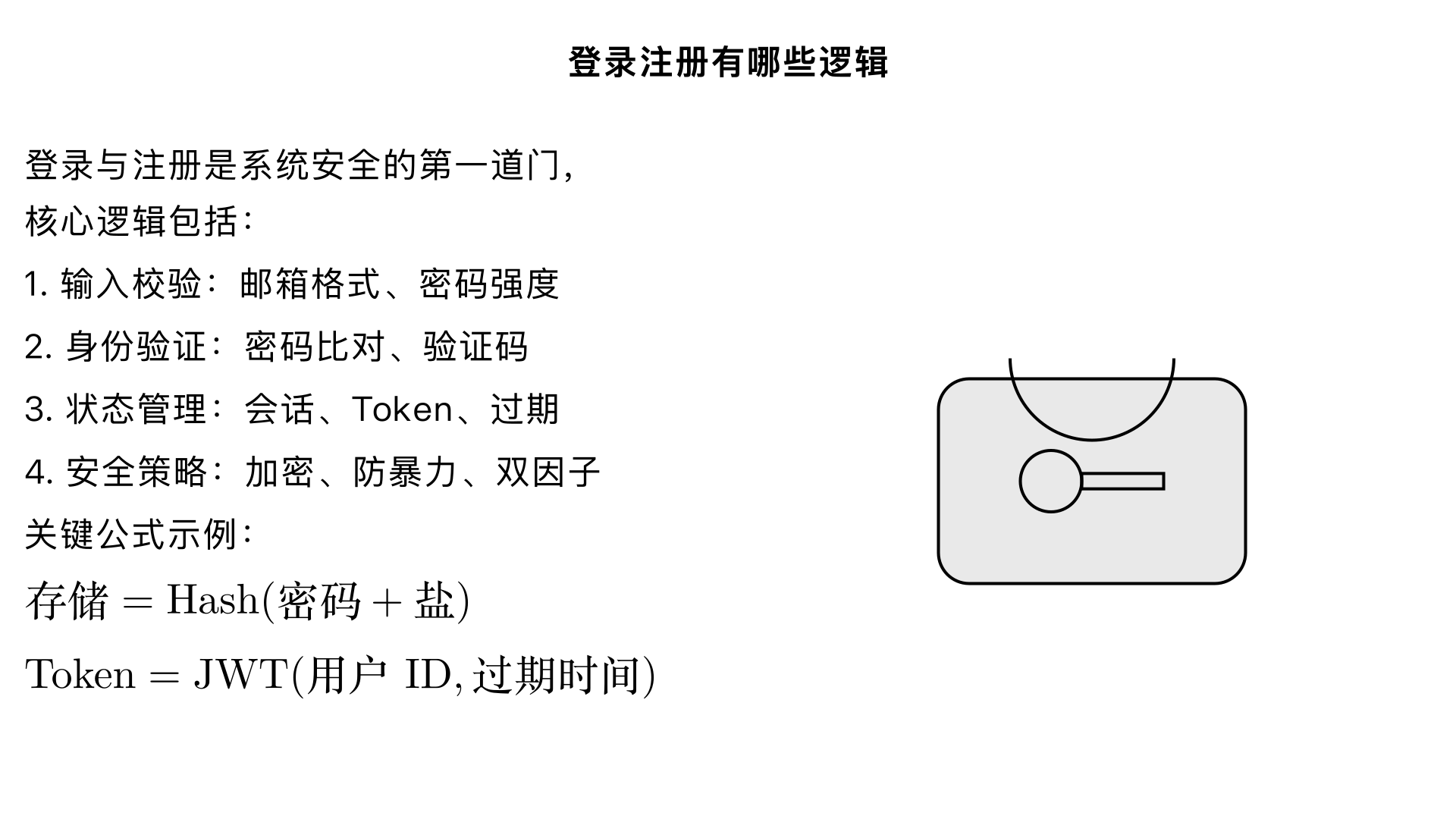
登录注册有那些逻辑

▶
遁与大壮——退隐与强盛的辩证法 一、遁卦(天山遁)——退隐的智慧 1. 卦序的承继 上一卦恒卦(雷风恒)讲恒久之道,但恒久并非永恒不变,物极必反,故继之以遁卦,表示退避。 《序卦传》:“恒者,久也。物不可以久居其所,故受之以遁。遁者,退也。” 2. 卦象解析 上乾(天)下艮(山):天下有山,山高而天退,象征退避。 金景芳分析:乾为刚健,艮为止,刚健而止,不轻进,有退避之象。 四阳二阴:阴气渐长,阳气渐消,象征小人道长,君子道消之时。 3. 《彖传》精讲 “遁,亨,遁而亨也。刚当位而应,与时行也。” “遁而亨”:退避而后能亨通。强调主动退避以保身、待时。 “刚当位而应”:指九五阳刚当位,与六二相应,象征君子虽处退时,但守正应时。 “与时行也”:根据时势行动,时当退则退。 “小利贞,浸而长也。” 阴气逐渐增长(浸而长),故只宜小利贞,不宜大有作为。 金景芳强调:遁卦并非消极逃避,而是“与时行”的积极智慧,如孔子所言“用之则行,舍之则藏”。 4. 《大象传》阐发 “天下有山,遁。君子以远小人,不恶而严。” “远小人”:远离小人,但非憎恶之极,而是保持距离。 “不恶而严”:不显露憎恶之情,但保持威严,界限分明。 金景芳联系历史:如柳下惠“直道而事人”,不因小人而改变原则,但也不激烈对抗。 5. 爻辞精析 遁卦爻辞体现了不同境遇下的退避策略。 初六:遁尾,厉,勿用有攸往。 “遁尾”:退避时落在最后,危险。 象征:退避不及时,陷入被动。 爻象:初六阴爻在遁卦之初,阴气未盛,本当早退,却迟疑落尾。 六二:执之用黄牛之革,莫之胜说。 “执之”:固结、牵制。 “黄牛之革”:黄色中色,牛革坚韧,喻以中正坚固之志固守不退。 爻象:六二柔中得正,与九五相应,在遁之时,因有应于君,不必急退,可坚守岗位。 九三:系遁,有疾厉,畜臣妾吉。 “系遁”:心有系恋,不能退避。 “有疾厉”:有疾病危险。 “畜臣妾吉”:若像管理臣妾小事那样,则吉(意为若退避不决,则只宜料理小事)。 金景芳分析:九三阳爻居刚位,与上九无应,且紧邻六二(阴爻),有被牵系之象。 九四:好遁,君子吉,小人否。 “好遁”:喜好退避(或时机好而退)。 君子能超然退避,故吉;小人恋栈,故否。 爻象:九四阳居阴位,刚而能柔,与初六相应却能舍之而退,故为“好遁”。 九五:嘉遁,贞吉。 “嘉遁”:美好的退避。 爻象:九五刚中居尊,与六二相应,却能适时退避,为退避之楷模。 金景芳举例:尧舜禅让,功成身退。 上九:肥遁,无不利。 “肥遁”:高飞远遁,无所不利。 爻象:上九处遁之极,远离阴爻,无牵无挂,故能洒脱退避。 6. 遁卦总结 遁卦教导我们在小人道长、形势不利时,应果断退避,但退避有智慧:及时(避免遁尾)、坚定(如黄牛之革)、洒脱(好遁、嘉遁、肥遁)。金景芳强调,遁卦是“君子以俭德辟难”,与道家隐退不同,儒家退避是为了守道待时。 二、大壮卦(雷天大壮)——强盛之道 1. 卦序的递进 遁卦是退避,但退避不是永远,物极必反,阳气复盛,故继之大壮卦。 《序卦传》:“遁者退也。物不可以终遁,故受之以大壮。” 2. 卦象解析 上震(雷)下乾(天):雷在天上,声势浩大,强壮之象。 四阳二阴:阳爻过半,阳气强盛,故称“大壮”。 金景芳分析:大壮并非仅指力量强大,更指“刚以动”,即刚健而能行动,但需守礼(非礼弗履)。 3. 《彖传》精讲 “大壮,大者壮也。刚以动,故壮。” 解释卦名:阳为大,阳爻过半故壮。 “刚以动”:下乾刚健,上震行动,刚健而行动,所以强壮。 “大壮利贞,大者正也。正大而天地之情可见矣。” 大壮利于守正,因为强大者必须正(否则恃强凌弱)。 “正大”即正义而强大,由此可见天地之情(天理)。 金景芳阐发:儒家主张“以德服人”,反对“以力服人”,大壮必须配以正道。 4. 《大象传》阐发 “雷在天上,大壮。君子以非礼弗履。” 雷在天上,声势壮盛,但君子观此象,却强调“非礼弗履”(不符合礼的事不做)。 金景芳重点:强壮时最容易越礼,故需以礼约束。如孔子说“克己复礼”。 5. 爻辞精析 大壮卦爻辞多警示强盛时易犯的错误。 初九:壮于趾,征凶,有孚。 “壮于趾”:强壮在脚趾,喻微壮而躁动。 “征凶”:前进有凶险。 初九阳刚处下,急于上进,但位卑力弱,故凶。 九二:贞吉。 守正则吉。 九二阳居阴位,刚而能柔,且得中,故能守正。 九三:小人用壮,君子用罔,贞厉。羝羊触藩,羸其角。 关键爻辞,揭示全卦主旨。 “小人用壮”:小人恃强凌弱。 “君子用罔”:君子用无为(或解为“网”,喻智慧)应对。 “贞厉”:即使动机纯正也有危险。 “羝羊触藩,羸其角”:公羊撞篱笆,角被卡住,喻恃强冒进受挫。 金景芳阐发:强盛时不可任性,应知进退。 九四:贞吉,悔亡。藩决不羸,壮于大舆之輹。 “藩决不羸”:篱笆被撞破,角没被卡住。 “壮于大舆之輹”:像大车的轮輹一样强壮(能行)。 九四阳居阴位,刚而能柔,且已过中,有条件前进,但仍需守正。 六五:丧羊于易,无悔。 “丧羊于易”:在田边丧失了羊(象征丧失强壮)。 “无悔”:无悔。 六五阴居尊位,以柔制刚,主动减弱强壮,故无悔。 上六:羝羊触藩,不能退,不能遂,无攸利,艰则吉。 再次出现“羝羊触藩”,进退两难。 “艰则吉”:在艰难中自守则吉。 上六处壮之终,壮极则反,若知艰难谨慎,可化凶为吉。 6. 大壮卦总结 大壮卦强调强盛时必须守正、用柔、知止。金景芳指出,大壮卦与遁卦相反相成:遁卦讲退,大壮讲进;但大壮之进必须谨慎,否则反而招祸。这与老子“物壮则老”思想相通,但儒家更强调“礼”的约束。 三、遁与大壮的辩证关系 阴阳消长:遁卦阴长阳消,大壮卦阳长阴消,体现阴阳互变的规律。 进退智慧:遁卦讲适时而退,大壮讲适时而进,二者都强调“时”的重要性。 共同原则:无论进退,都要守正、有德。遁卦“君子以远小人”,大壮卦“非礼弗履”。
▶
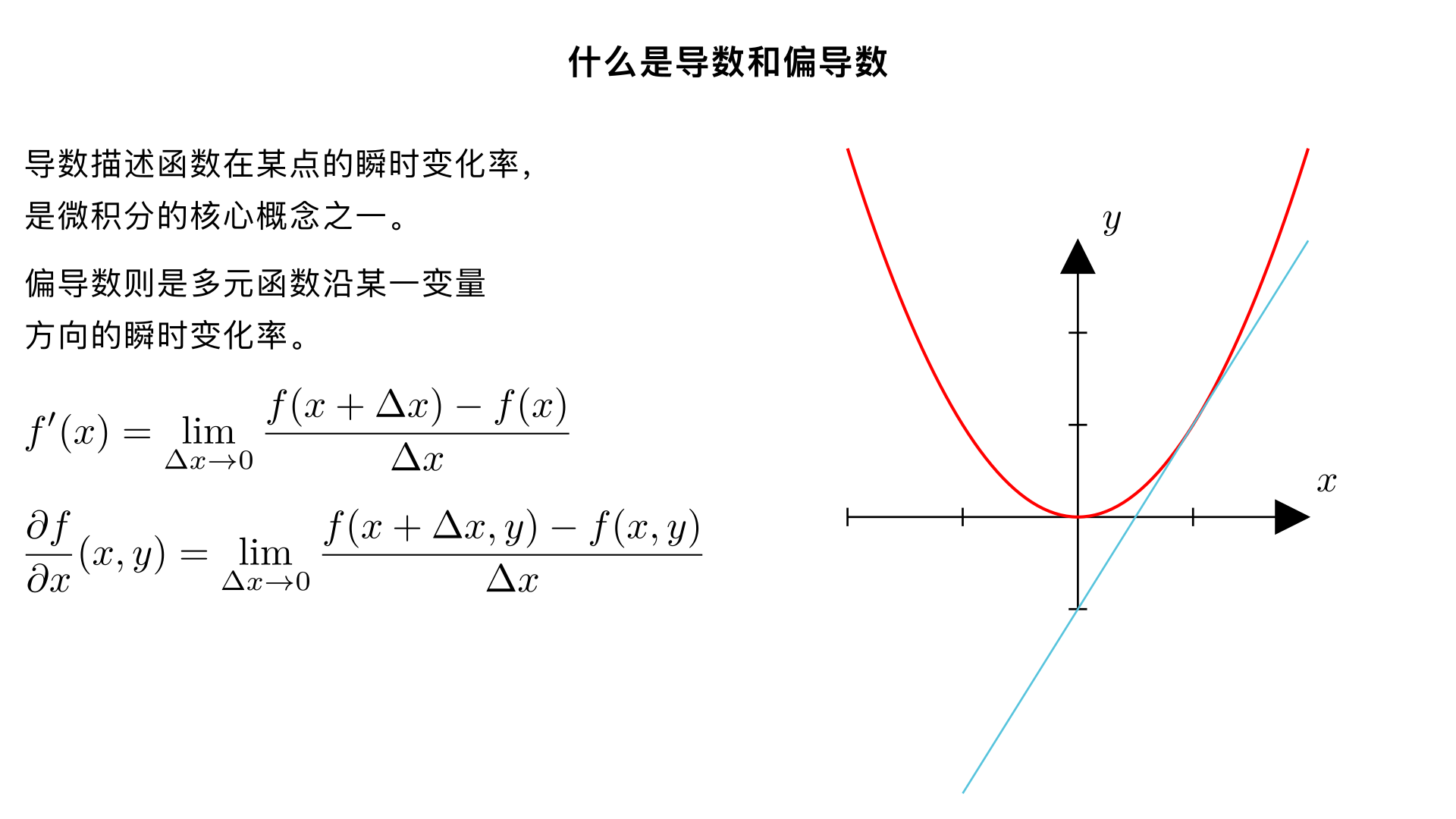
什么是导数和偏导数

▶
统筹规划:甲、乙、丙三人去李师傅处理发,甲剪发需20分钟,乙剪发需25分钟,丙烫发需60分钟。怎样安排他们的理发次序,才能使他们所花的总时间最短最短时间是多少 一、题型判断:统筹规划问题(小学奥数 “排队等候时间优化” 子类) 这类题型的核心是通过合理安排操作顺序,减少 “等候时间” 的总和。解题关键是遵循 “用时短的任务优先进行” 原则,让花费时间少的人先操作,从而降低其他人的等待时长,本质是 “时间资源的最优分配”。 二、解题过程(分 2 步:确定最优理发次序→计算总时间) 已知条件: 甲剪发:20 分钟,乙剪发:25 分钟,丙烫发:60 分钟; 总时间 = 每个人的理发时间 + 每个人的等候时间(等候时间指自己开始理发前,前面人理发的总耗时); 核心逻辑:要让总时间最短,需让理发时间短的人先理,减少后续人员的等待时长。 步骤 1:确定最优理发次序 比较三人理发时长:分钟<分钟<分钟因此最优次序为:甲先理→乙其次→丙最后 步骤 2:计算总时间(分阶段计算每人的耗时与等候时间) 甲理发时 甲理发时间:20 分钟; 乙、丙等候时间:各 20 分钟; 此阶段总耗时:20 分钟(无前置等待,甲直接开始)。 乙理发时 乙理发时间:25 分钟; 丙等候时间:25 分钟(甲已理完,丙只需等乙的时间); 此阶段累计耗时:20+25=45 分钟。 丙理发时 丙理发时间:60 分钟; 无后续等待人员; 此阶段累计耗时:45+60=105 分钟。 总时间验证(另一种计算方式:个人总耗时相加) 甲的总耗时(自己理发时间):20 分钟; 乙的总耗时(等甲 + 自己理发):20+25=45 分钟; 丙的总耗时(等甲 + 等乙 + 自己理发):20+25+60=105 分钟; 三人总时间总和:20+45+105=170 分钟; 注:题目问的 “总时间”,若指从开始到最后结束的总时长,是 105 分钟;若指三人花费的时间总和,是 170 分钟。小学奥数中此类题默认问从开始到结束的最短总时长。 三、反推验证(对比其他次序,确认最优) 验证最优次序的合理性若次序改为 “乙→甲→丙”: 总结束时长:25+20+60=105 分钟(结束时长相同,但三人总耗时总和会增加:25+(25+20)+(25+20+60)=175 分钟);若次序改为 “丙→甲→乙”: 总结束时长:60+20+25=105 分钟,三人总耗时总和会大幅增加:60+(60+20)+(60+20+25)=245 分钟;结论:甲→乙→丙的次序,三人总耗时总和最少(170 分钟),是最优方案。 时间逻辑验证 甲先理 20 分钟→乙接着理 25 分钟(此时累计 45 分钟)→丙接着理 60 分钟(累计 105 分钟),流程无等待空档,时间利用最充分 ✔️; 等候时间计算无重复、无遗漏,符合 “短任务优先” 的统筹原则 ✔️。 四、最终结果 最优理发次序:甲→乙→丙

▶