T
Teach Me AnythingTMA
Video History
Page 4 / 126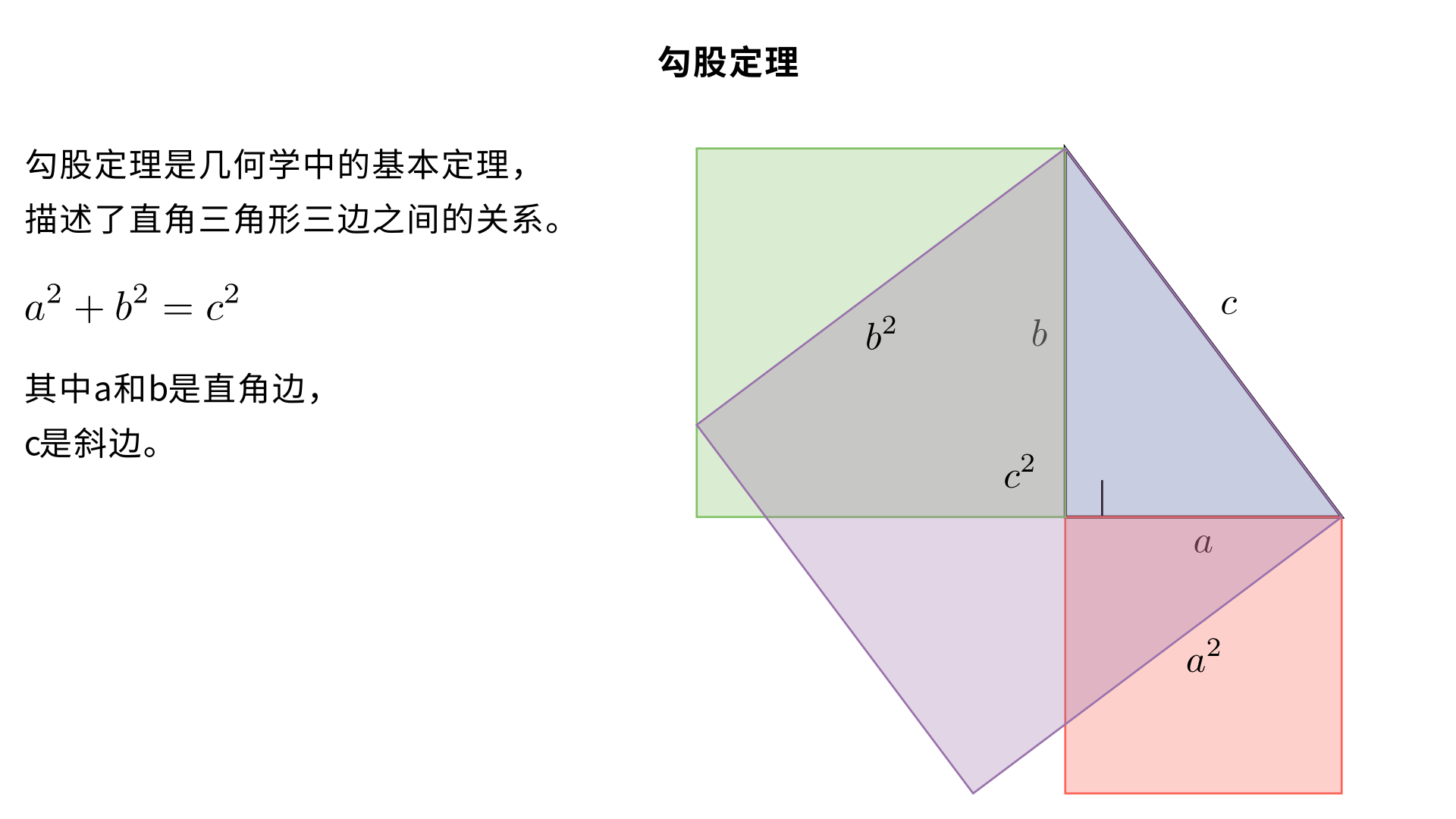
▶
勾股定理
▶
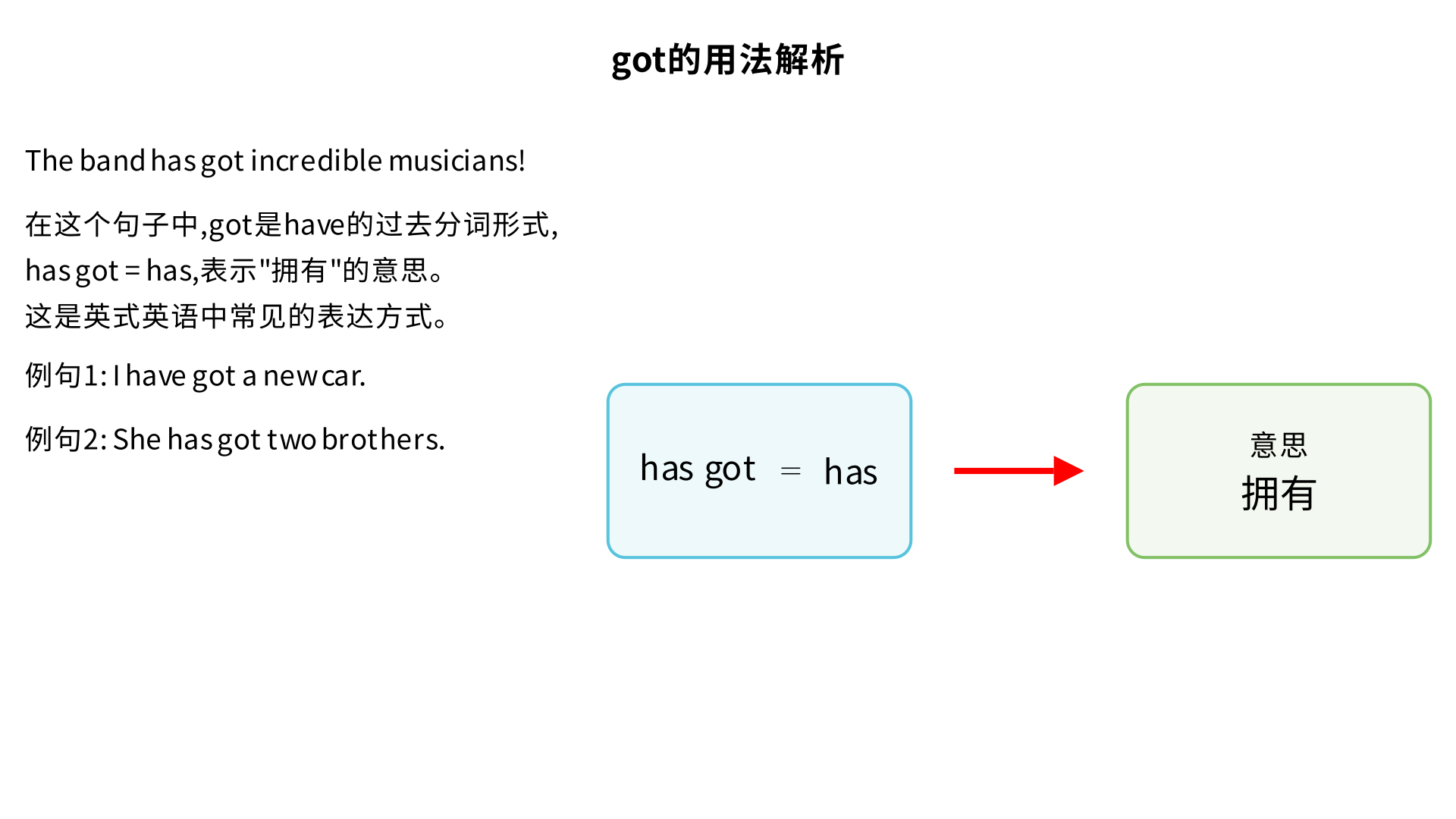
解释句子 The band has got incredible musicians! got在这里是什么意思?

▶
人们如何预测天气变化
▶
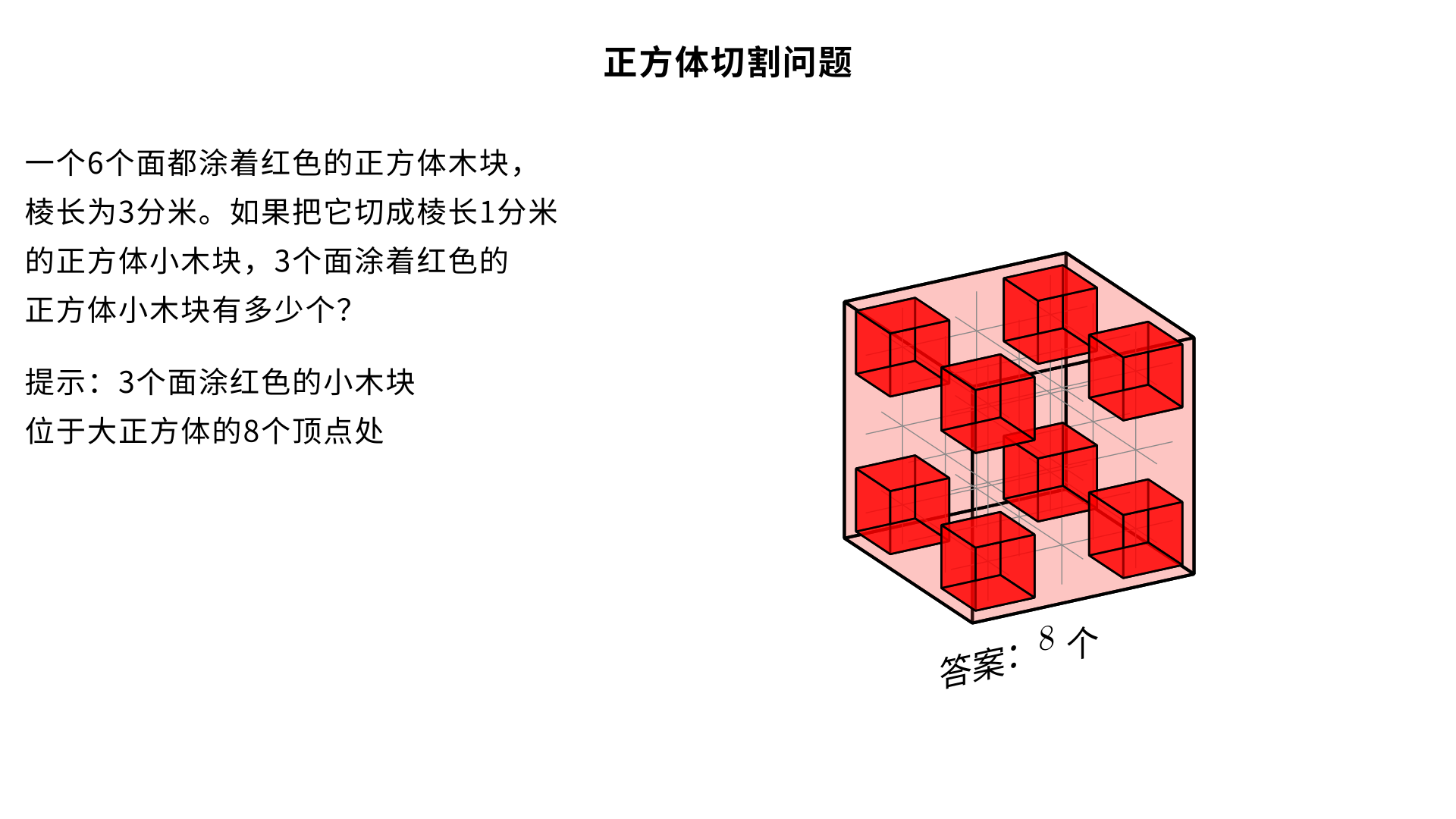
一个6个面都涂着红色的正方体木块,棱长为3分米。如果把它切成棱长1分米的正方体小木块,3个面涂着红色的正方体小木块有( )个
▶
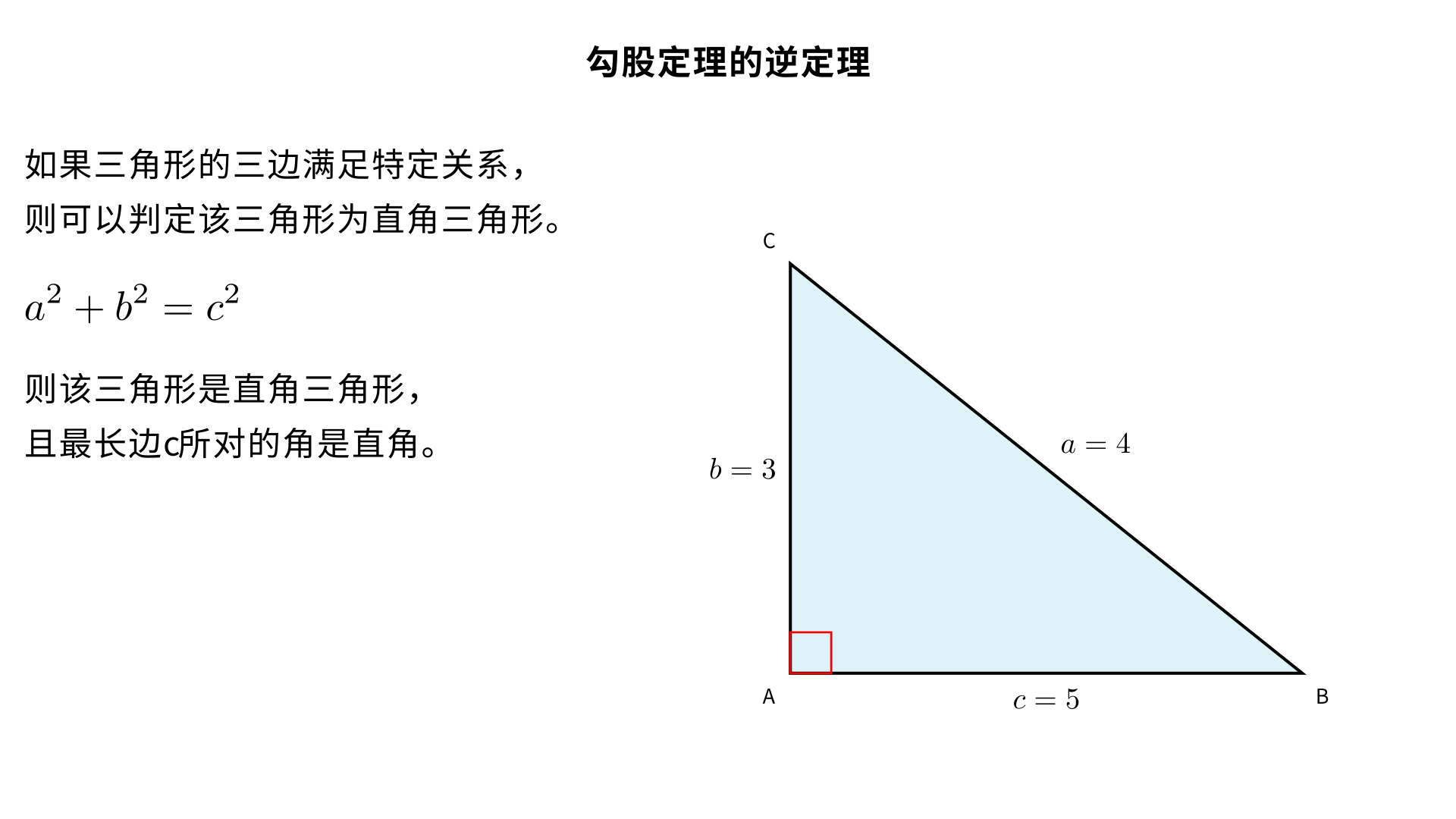
勾股定理的逆定理 本知识点属于八年级数学几何板块,是判断一个三角形是否为直角三角形的核心方法,与勾股定理互为逆定理。 一、 定义(核心结论) 如果一个三角形的三条边长 a 、 b 、 c 满足关系: a 2 +b 2 =c 2 那么这个三角形是直角三角形,且最长边 c 所对的角是直角。 补充:互逆命题关系 勾股定理(原命题):直角三角形中,两直角边的平方和等于斜边的平方(由 “直角三角形” 得 “三边关系”)。 勾股定理的逆定理(逆命题):三角形三边满足 a 2 +b 2 =c 2 ,则这个三角形是直角三角形(由 “三边关系” 得 “直角三角形”)。 二、 判定直角三角形的步骤 确定最长边:找出三角形三边中的最长边,记为 c ; 计算平方和:分别计算两条较短边的平方和 a 2 +b 2 ,以及最长边的平方 c 2 ; 比较判断: 若 a 2 +b 2 =c 2 → 该三角形是直角三角形; 若 a 2 +b 2 =c 2 → 该三角形不是直角三角形。 三、 典型例题 例题 1:基础判定 判断边长为 3、4、5 的三角形是否为直角三角形。解: 最长边为 5,记 c=5 , a=3 , b=4 ; 计算: a 2 +b 2 =3 2 +4 2 =9+16=25 , c 2 =5 2 =25 ; 因为 3 2 +4 2 =5 2 ,所以这个三角形是直角三角形,且最长边 5 所对的角是直角。 例题 2:非整数边长判定 判断边长为 2 、 3 、 5 的三角形是否为直角三角形。解: 最长边为 5 ,记 c= 5 , a= 2 , b= 3 ; 计算: a 2 +b 2 =( 2 ) 2 +( 3 ) 2 =2+3=5 , c 2 =( 5 ) 2 =5 ; 因为 a 2 +b 2 =c 2 ,所以这个三角形是直角三角形。 四、 易错点提醒 未确定最长边直接计算:比如三边为 5、12、13,若误把 12 当作最长边计算 5 2 +13 2 ,会得到错误结论; 混淆勾股定理与逆定理的用途:勾股定理用于已知直角三角形求边长;逆定理用于已知三边长判断三角形形状; 忽略 “最长边对直角”:满足 a 2 +b 2 =c 2 时,只有最长边 c 对应的角是直角,不是任意边。
▶
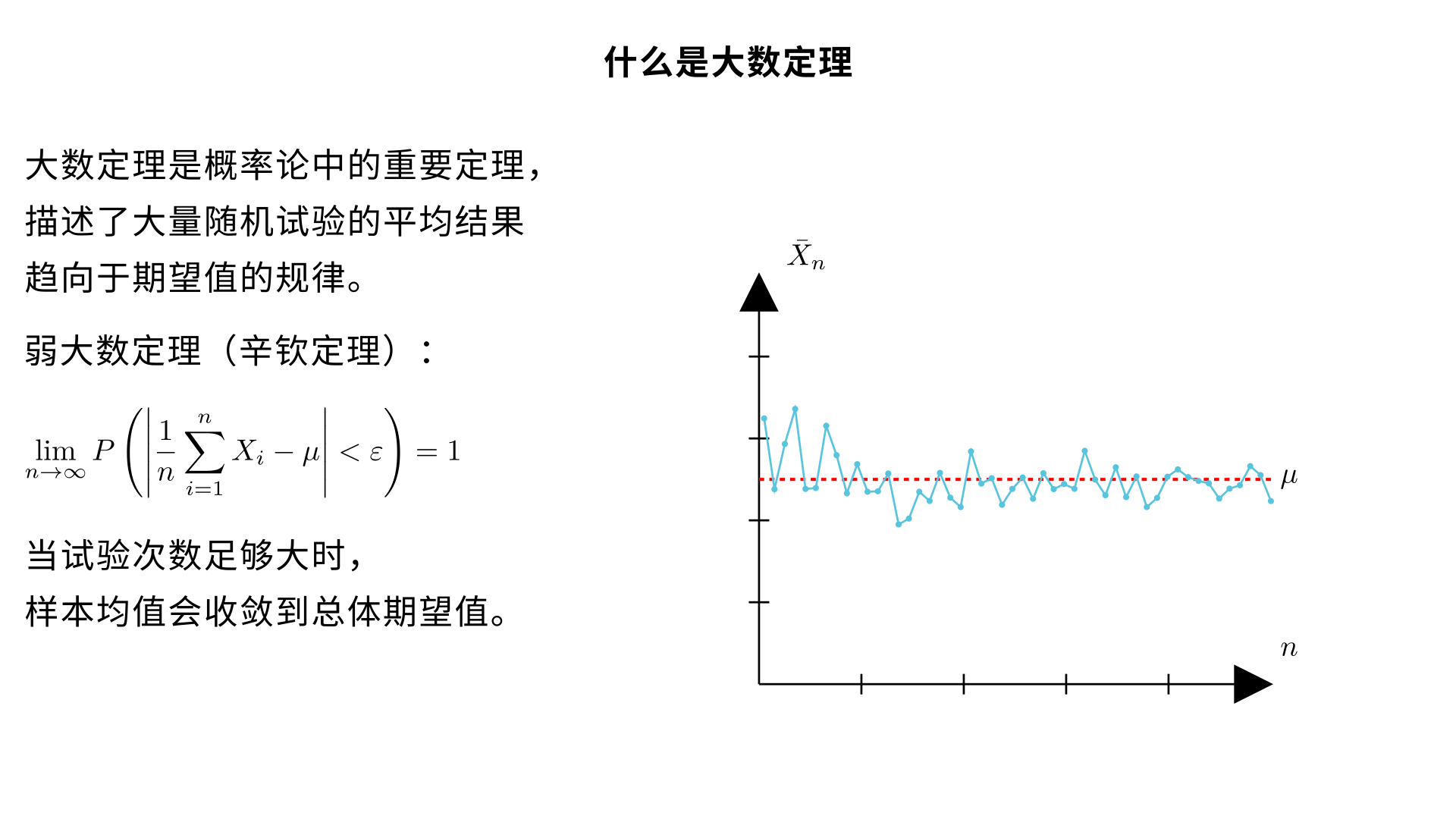
什么事大数定理
▶
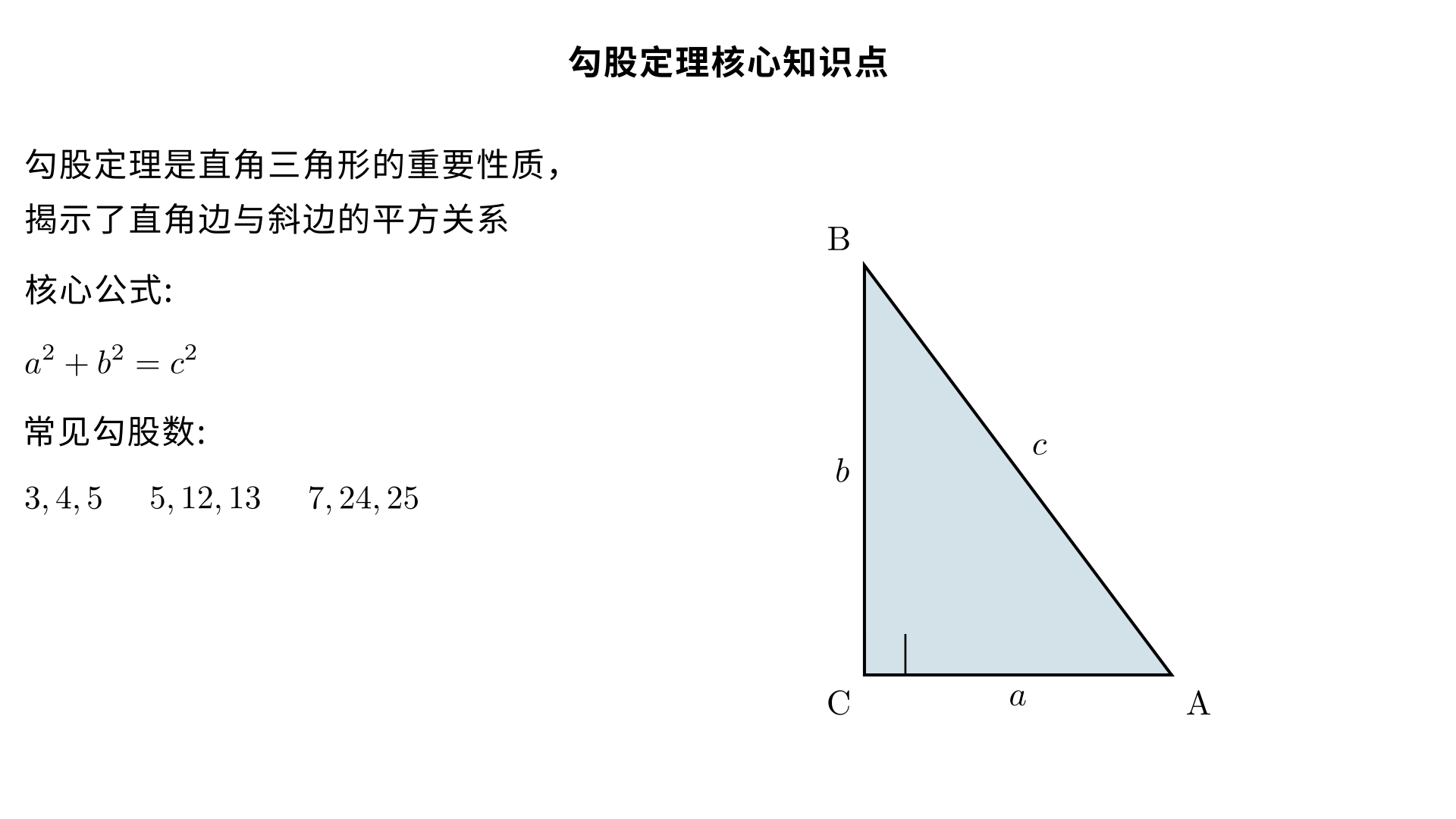
八年级数学 勾股定理 核心知识点(系统化拆解) 勾股定理是八年级几何的核心定理,也是直角三角形的重要性质,主要解决直角三角形的边长计算和线段平方关系证明问题,以下按定义→公式→验证→注意事项→常见勾股数→典型例题→解题步骤拆解,贴合八年级教材要求。 一、勾股定理的定义 在直角三角形中,两条直角边的平方和等于斜边的平方。 边的命名约定 设直角三角形的两条直角边长度分别为 a 、 b ,斜边(直角所对的边,最长边)长度为 c ,则勾股定理的核心表述围绕此三边展开。 二、核心公式及变形(必考) 1. 基本公式 a 2 +b 2 =c 2 (直角边 ² + 直角边 ² = 斜边 ²) 2. 常用变形公式(已知两边求第三边,直接套用) 求斜边: c= a 2 +b 2 求直角边 a : a= c 2 −b 2 求直角边 b : b= c 2 −a 2 ✅ 关键前提:仅适用于直角三角形,非直角三角形不能直接使用。 三、勾股定理的验证(教材重点,面积法核心) 勾股定理的验证本质是利用图形的面积相等推导,八年级要求掌握面积法,以下 3 种经典验证方法(赵爽弦图为必考): 1. 赵爽弦图(我国古代数学家赵爽证明,教材核心) 以直角三角形的斜边为边长作大正方形,内部用 4 个全等的直角三角形拼出小正方形,通过大正方形面积 = 4 个直角三角形面积 + 小正方形面积推导,是中考常考的证明素材。 2. 毕达哥拉斯证法 用两个全等的直角三角形拼出直角梯形,通过梯形面积 = 三个直角三角形面积和推导,核心仍是面积相等。 3. 总统证法(伽菲尔德证法) 与毕达哥拉斯证法思路一致,简化了梯形的拼接方式,步骤更简洁,适合八年级基础证明。 四、适用范围与核心注意事项(避错关键) 仅适用于直角三角形:锐角三角形、钝角三角形的三边不满足此关系; 斜边是前提:公式中 c 一定是斜边(最长边),若题目未明确边的类型,需分类讨论; 边长为正数:计算结果中,边长的算术平方根为正,舍去负根; 平方关系≠边长关系:注意区分 a 2 +b 2 =c 2 和 a+b=c ,后者一定不成立; 勾股定理是 “性质”:是已知直角三角形,推导三边平方关系,与后续 “勾股定理的逆定理(判定直角三角形)” 区分开。 五、常见勾股数(速算必备,八年级常考) 勾股数:满足 a 2 +b 2 =c 2 的正整数组 (a,b,c) ,核心勾股数及变形需熟记,解题可直接套用: 1. 基础勾股数(核心三组,必考) 3, 4, 5(最常用) 5, 12, 13 7, 24, 25 2. 勾股数的倍数性质 若 (a,b,c) 是勾股数,则其正整数倍 (ka,kb,kc) ( k>0 ,整数)也是勾股数,例如: 3,4,5 的 2 倍:6,8,10;3 倍:9,12,15 5,12,13 的 2 倍:10,24,26 ✅ 注意:1,2,3 不是勾股数( 1 2 +2 2 =3 2 ),勾股数需严格满足平方和关系。 六、典型例题(分类型,含解题步骤,贴合八年级考题) 勾股定理的考题分基础计算型、分类讨论型、实际应用型,是八年级同步练习的核心题型,以下各举一例,步骤按 “审题→定直角→标边→套公式” 展开。 类型 1:基础计算 —— 已知直角三角形两边,求第三边 例题:在 Rt△ABC 中,∠C=90°,若 a=3 , b=4 ,求斜边 c ;若 c=10 , a=6 ,求直角边 b 。解题步骤: 审题:∠C=90°,确定 c 为斜边, a,b 为直角边; 套公式: 求 c : c= 3 2 +4 2 = 25 =5 ; 求 b : b= 10 2 −6 2 = 64 =8 。 类型 2:分类讨论 —— 未明确 “斜边 / 直角边”,需分情况 例题:在 Rt△ABC 中,一条边长为 5,另一条边长为 12,求第三边的长。解题步骤: 审题:未明确直角边 / 斜边,第三边可能是斜边或直角边,分两种情况; 情况 1:12 为斜边,5 为直角边,第三边 x 为直角边: x= 12 2 −5 2 = 119 ; 情况 2:12 和 5 均为直角边,第三边 x 为斜边: x= 12 2 +5 2 =13 ; 结论:第三边长为 13 或 119 。 类型 3:实际应用 —— 将实际问题转化为 “直角三角形边长计算” 例题:一架长 10m 的梯子,斜靠在竖直的墙上,梯子底端离墙 6m,求梯子顶端到地面的高度。解题步骤: 转化:梯子为斜边(10m),底端离墙的距离为一条直角边(6m),顶端高度为另一条直角边(设为 h ); 套公式: h= 10 2 −6 2 =8 ; 结论:梯子顶端到地面的高度为 8m。 七、勾股定理核心解题步骤(通用) 无论基础题还是应用题,均遵循以下 4 步,可避免漏解、错解: 找直角:确定直角三角形的直角顶点,明确直角边和斜边(无直角则需构造直角,如折叠问题); 标边长:将已知边长标注在对应边上,未知边设为 x ; 套公式:根据勾股定理写等式,代入已知数; 算结果:求解方程,舍去负根(边长为正),有多种情况需分类讨论。
▶
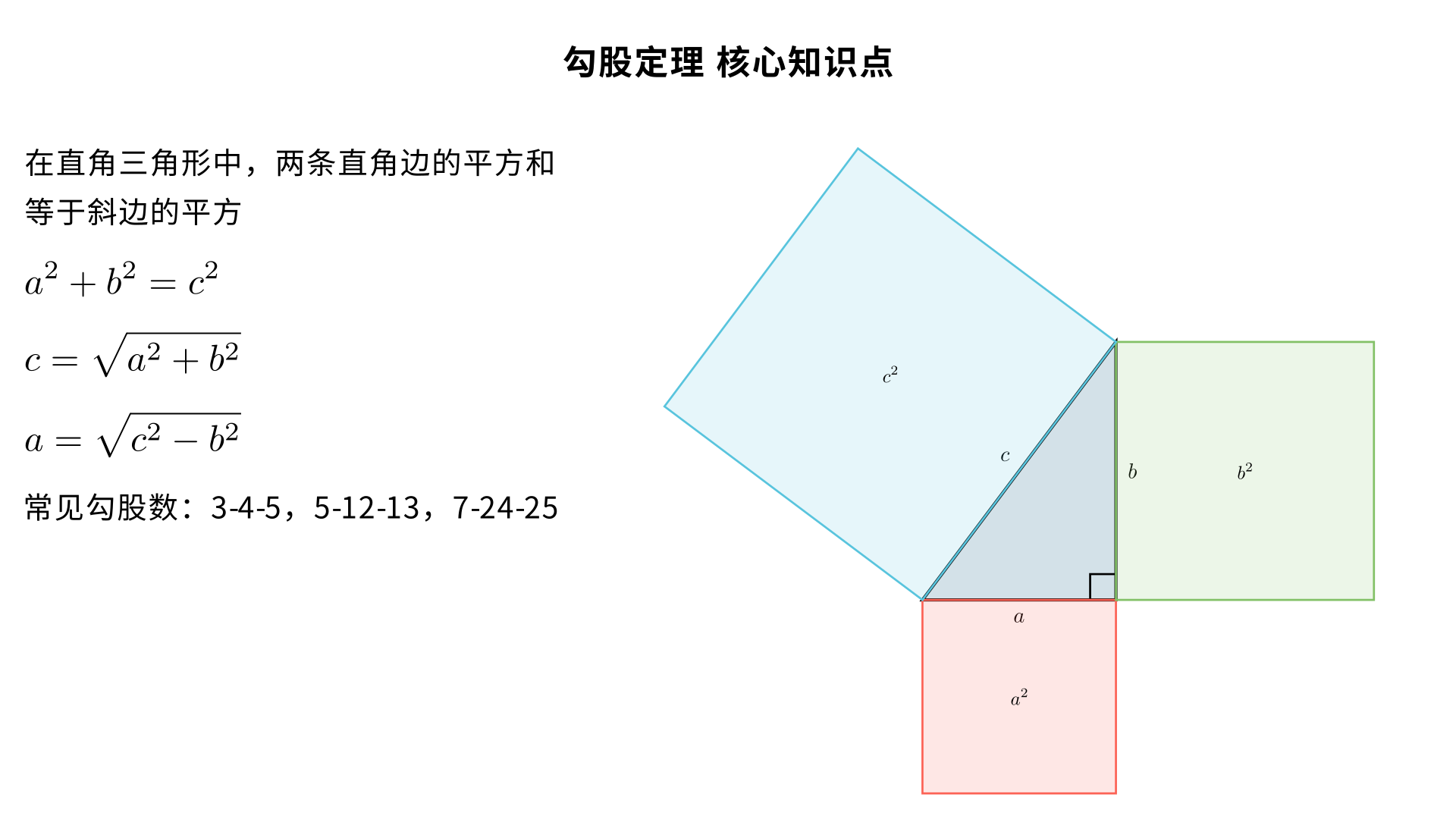
八年级数学 勾股定理 核心知识点 一、勾股定理的定义 在直角三角形中,两条直角边的平方和等于斜边的平方。 边的命名约定 设直角三角形的两条直角边长度分别为 a、b,斜边(直角所对的边,最长边)长度为c,则勾股定理的核心表述围绕此三边展开。 二、核心公式及变形(必考) 1. 基本公式 a²+b²=c²(直角边 ² + 直角边 ² = 斜边 ²) 2. 常用变形公式(已知两边求第三边,直接套用) 求斜边c:c=根号下a²+b² 求直角边a:a=根号下c²−b² 求直角边b:b=根号下c²−a² ✅ 关键前提:仅适用于直角三角形,非直角三角形不能直接使用。 三、勾股定理的验证(教材重点,面积法核心) 勾股定理的验证本质是利用图形的面积相等推导,八年级要求掌握面积法,以下 3 种经典验证方法(赵爽弦图为必考): 1. 赵爽弦图(我国古代数学家赵爽证明,教材核心) 以直角三角形的斜边为边长作大正方形,内部用 4 个全等的直角三角形拼出小正方形,通过大正方形面积 = 4 个直角三角形面积 + 小正方形面积推导,是中考常考的证明素材。 2. 毕达哥拉斯证法 用两个全等的直角三角形拼出直角梯形,通过梯形面积 = 三个直角三角形面积和推导,核心仍是面积相等。 3. 总统证法(伽菲尔德证法) 与毕达哥拉斯证法思路一致,简化了梯形的拼接方式,步骤更简洁,适合八年级基础证明。 四、适用范围与核心注意事项(避错关键) 仅适用于直角三角形:锐角三角形、钝角三角形的三边不满足此关系; 斜边是前提:公式中c一定是斜边(最长边),若题目未明确边的类型,需分类讨论; 边长为正数:计算结果中,边长的算术平方根为正,舍去负根; 平方关系≠边长关系:注意区分a²+b²=c²和a+b=c,后者一定不成立; 勾股定理是 “性质”:是已知直角三角形,推导三边平方关系,与后续 “勾股定理的逆定理(判定直角三角形)” 区分开。 五、常见勾股数(速算必备,八年级常考) 勾股数:满足a²+b²=c²的正整数组(a,b,c),核心勾股数及变形需熟记,解题可直接套用: 1. 基础勾股数(核心三组,必考) 3, 4, 5(最常用) 5, 12, 13 7, 24, 25 2. 勾股数的倍数性质 若(a,b,c)是勾股数,则其正整数倍(ka,kb,kc)(k>0,整数)也是勾股数,例如: 3,4,5 的 2 倍:6,8,10;3 倍:9,12,15 5,12,13 的 2 倍:10,24,26 ✅ 注意:1,2,3 不是勾股数,勾股数需严格满足平方和关系。

▶
勾股定理

▶
八年级数学 二次根式的加减 本模块核心围绕同类二次根式的判定和二次根式的加减运算法则展开,是二次根式运算的基础,也是后续学习二次根式混合运算的关键,整体遵循 “先化简,再合并” 的核心思路,和整式的加减(合并同类项)逻辑高度一致。 一、前置基础:同类二次根式(加减的前提) 1. 定义 几个最简二次根式,如果被开方数相同,那么这几个二次根式叫做同类二次根式。✅ 举例: 2 和 3 2 、 2 3 和 5 3 、 8 (非最简)和 2 (化简后是同类)都是同类二次根式;❌ 反例: 2 和 3 (被开方数不同)、 5 和 2 10 (被开方数不同)不是同类二次根式。 2. 关键判定步骤 判断两个 / 多个二次根式是否为同类,必须先化为最简二次根式,再看被开方数是否相同,缺一不可。例:判断 12 和 27 是否为同类二次根式解: 12 =2 3 , 27 =3 3 ,化简后被开方数都是 3,因此是同类二次根式。 3. 注意 同类二次根式只与最简后的被开方数有关,与根号外的系数无关; 一个二次根式的同类二次根式有无数个(如 3 的同类有 k 3 , k 为任意非零实数); 常数项(如 2、5)是特殊的 “同类项”,加减时直接合并常数即可。 二、核心法则:二次根式的加减运算法则 1. 法则内容 二次根式相加减,先把各个二次根式化为最简二次根式,再把同类二次根式分别合并,非同类二次根式不能合并。 2. 核心步骤(三步法) 第一步:化—— 将所有二次根式化为最简二次根式(满足:被开方数不含分母、被开方数中不含能开得尽方的因数或因式);第二步:找—— 找出化简后式子中的同类二次根式,用括号或下划线标注,非同类保持原式;第三步:合—— 合并同类二次根式:根号不变,系数相加减(和整式合并同类项:字母和字母指数不变,系数相加减完全一致)。 3. 字母表示 若 a 是最简二次根式,则 m a ±n a =(m±n) a ( 、 为有理数, a≥0 )。
▶
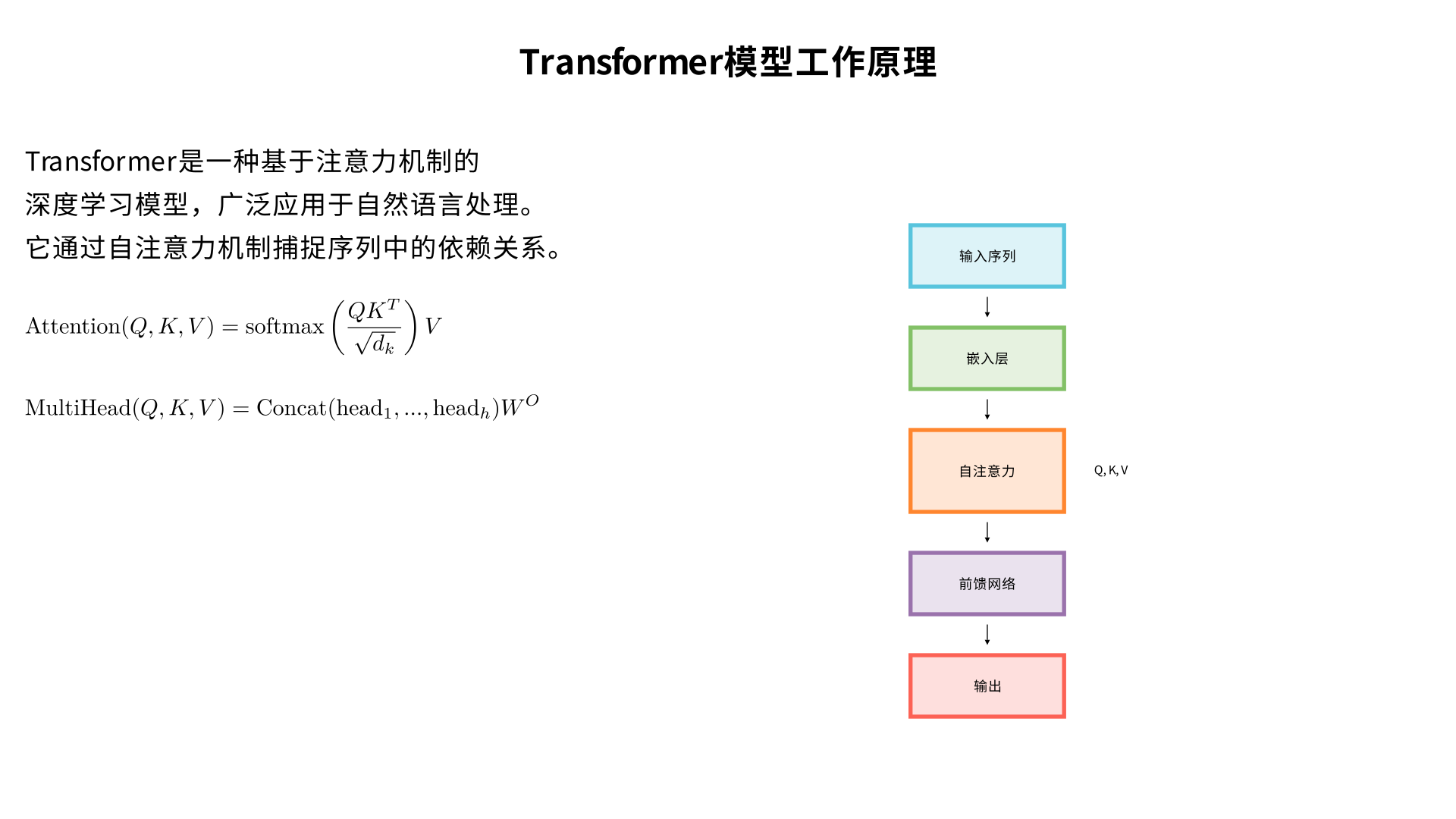
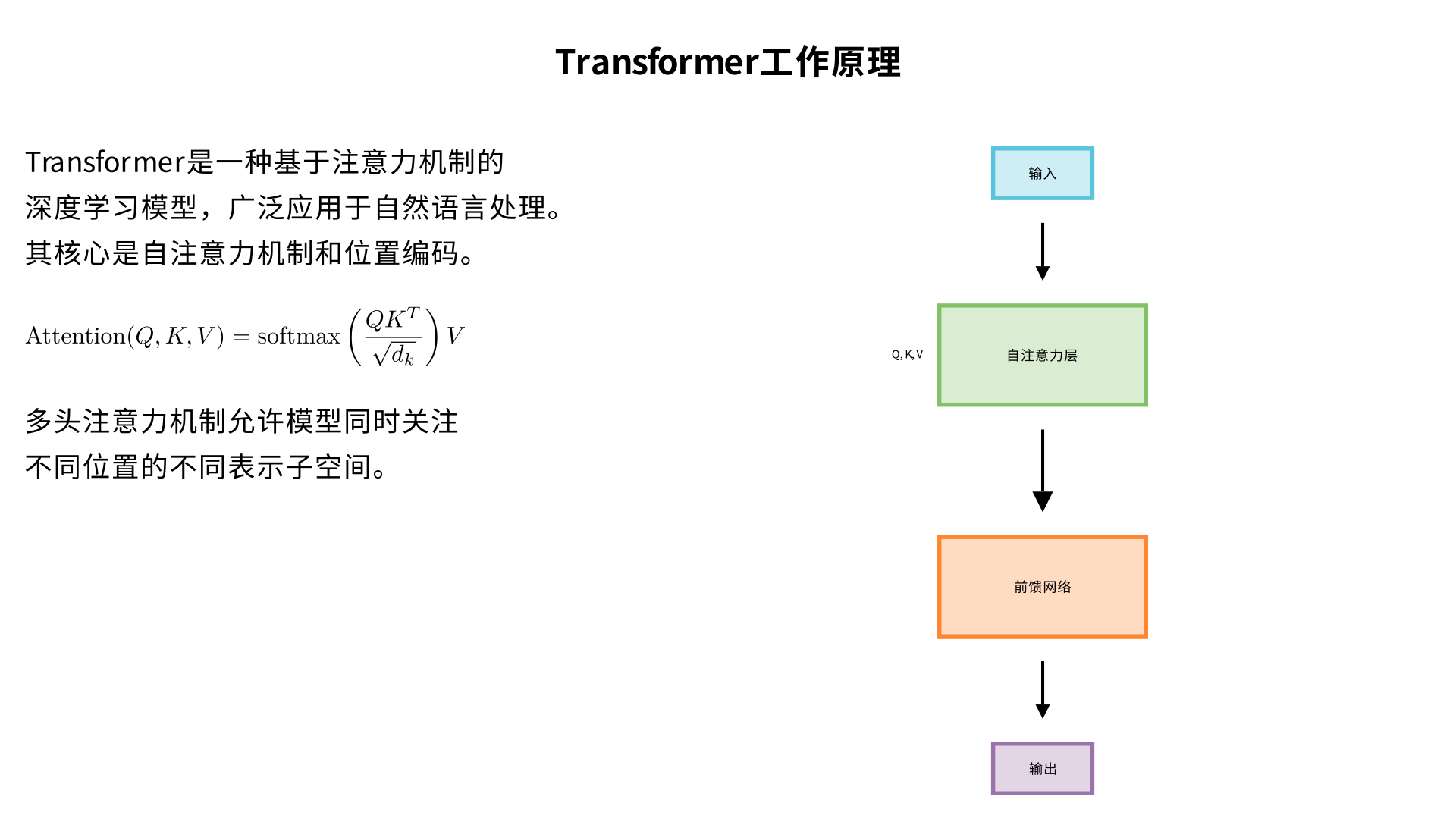
how the transformers work
▶