Teach Me Anything - AI Video Generator

$已知条件： •球队：甲、乙、丙、丁 4 支，每两队赛 1 场（单循环赛）； •无平局，每场 1 个胜者（总胜场数 = 总比赛场次）； •甲胜丁，且甲、乙、丙胜场数相同（设为x），求丁的胜场数（设为y）。步骤 1：计算 “总比赛场次” 与 “总胜场数” 单循环赛总场次公式：\frac{n(n-1)}{2}（n为球队数），代入n=4：总比赛场次 = \frac{4Ã3}{2}=6场因无平局，总胜场数 = 总比赛场次 = 6 场。步骤 2：建立 “胜场数关系” 并确定变量范围甲、乙、丙各胜x场，丁胜y场，总胜场数满足：3x + y = 6（x、y为非负整数，且x需符合实际比赛逻辑）结合 “甲胜丁” 的条件，推导x的可能值： •甲的对手是乙、丙、丁，甲至少胜 1 场（胜丁），故x \geq 1； •若x=1：则3Ã1 + y=6→y=3。但丁要胜 3 场，需打败甲、乙、丙，可题目明确 “甲胜丁”，丁不可能胜甲，矛盾，排除； •若x=2：则3Ã2 + y=6→y=0。此时需验证是否合理：甲胜 2 场（含胜丁，另 1 场胜乙或丙），乙胜 2 场（对手为甲、丙、丁，胜丁 + 胜甲 / 丙），丙胜 2 场（对手为甲、乙、丁，胜丁 + 胜甲 / 乙），无矛盾（例：甲胜丁 + 乙，乙胜丁 + 丙，丙胜丁 + 甲，丁全负）； •若x=3：则3Ã3=9 > 6，总胜场超 6，不可能，排除。步骤 3：确定丁的胜场数唯一符合条件的是y=0，即丁胜 0 场。三、反推验证（确保无逻辑矛盾）假设丁胜 1 场：则3x=6-1=5，x不是整数（胜场数需为整数），矛盾；假设丁胜 2 场：则3x=6-2=4，x不是整数，矛盾；假设丁胜 3 场：需胜甲、乙、丙，但 “甲胜丁”，不可能，矛盾；只有丁胜 0 场时，x=2（甲、乙、丙各胜 2 场），且满足 “甲胜丁”，所有比赛逻辑闭环（如：甲胜丁 + 乙，乙胜丁 + 丙，丙胜丁 + 甲），无矛盾。四、最终结果丁胜了 0 场。$

▶

已知条件： •球队：甲、乙、丙、丁 4 支，每两队赛 1 场（单循环赛）； •无平局，每场 1 个胜者（总胜场数 = 总比赛场次）； •甲胜丁，且甲、乙、丙胜场数相同（设为x），求丁的胜场数（设为y）。步骤 1：计算 “总比赛场次” 与 “总胜场数” 单循环赛总场次公式：\frac{n(n-1)}{2}（n为球队数），代入n=4：总比赛场次 = \frac{4Ã3}{2}=6场因无平局，总胜场数 = 总比赛场次 = 6 场。步骤 2：建立 “胜场数关系” 并确定变量范围甲、乙、丙各胜x场，丁胜y场，总胜场数满足：3x + y = 6（x、y为非负整数，且x需符合实际比赛逻辑）结合 “甲胜丁” 的条件，推导x的可能值： •甲的对手是乙、丙、丁，甲至少胜 1 场（胜丁），故x \geq 1； •若x=1：则3Ã1 + y=6→y=3。但丁要胜 3 场，需打败甲、乙、丙，可题目明确 “甲胜丁”，丁不可能胜甲，矛盾，排除； •若x=2：则3Ã2 + y=6→y=0。此时需验证是否合理：甲胜 2 场（含胜丁，另 1 场胜乙或丙），乙胜 2 场（对手为甲、丙、丁，胜丁 + 胜甲 / 丙），丙胜 2 场（对手为甲、乙、丁，胜丁 + 胜甲 / 乙），无矛盾（例：甲胜丁 + 乙，乙胜丁 + 丙，丙胜丁 + 甲，丁全负）； •若x=3：则3Ã3=9 > 6，总胜场超 6，不可能，排除。步骤 3：确定丁的胜场数唯一符合条件的是y=0，即丁胜 0 场。三、反推验证（确保无逻辑矛盾）假设丁胜 1 场：则3x=6-1=5，x不是整数（胜场数需为整数），矛盾；假设丁胜 2 场：则3x=6-2=4，x不是整数，矛盾；假设丁胜 3 场：需胜甲、乙、丙，但 “甲胜丁”，不可能，矛盾；只有丁胜 0 场时，x=2（甲、乙、丙各胜 2 场），且满足 “甲胜丁”，所有比赛逻辑闭环（如：甲胜丁 + 乙，乙胜丁 + 丙，丙胜丁 + 甲），无矛盾。四、最终结果丁胜了 0 场。

Teach Me AnythingTMA

Video History

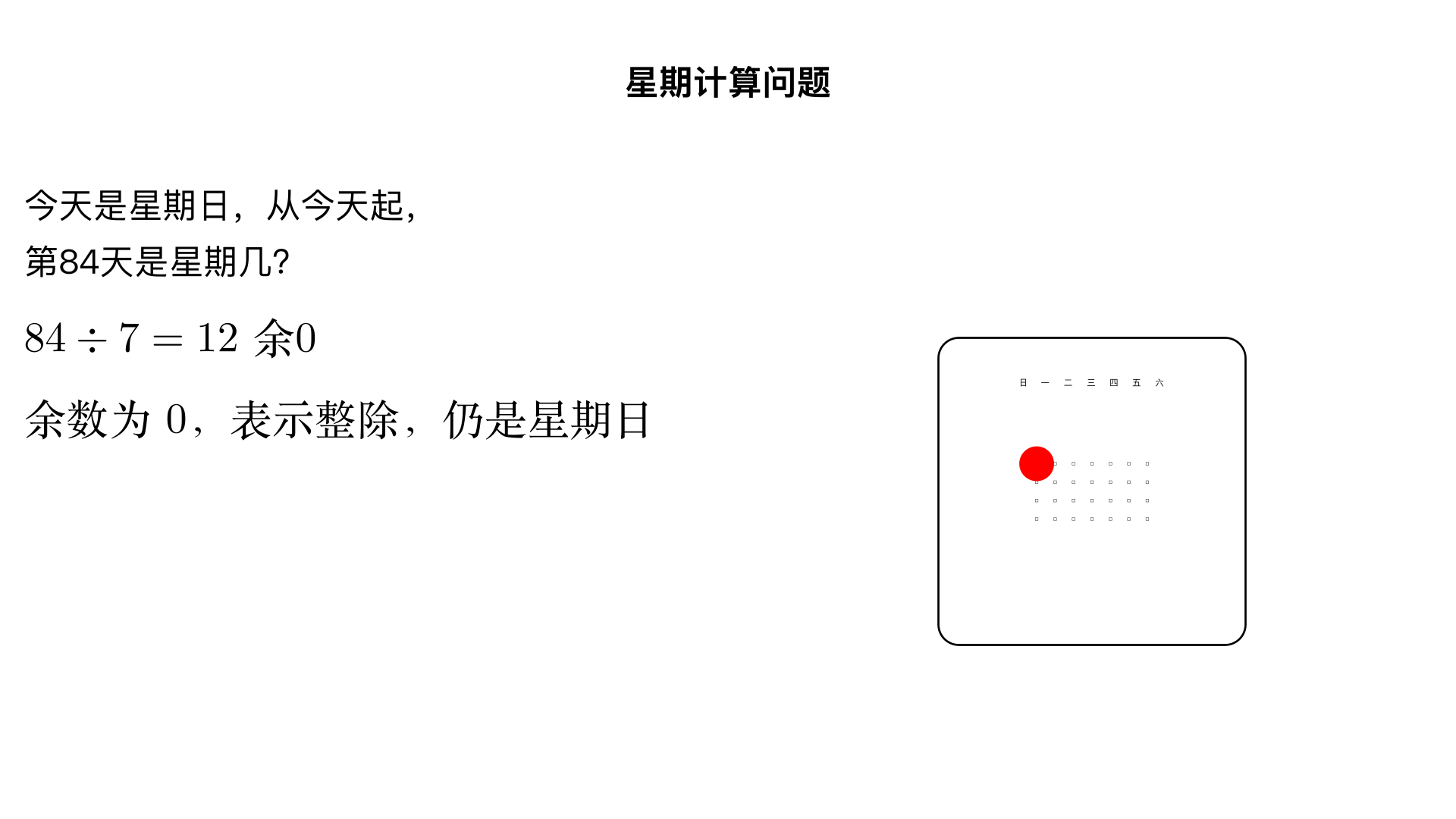
今天是星期日,从今天起,第84天是星期几?

七年级物理科学探究的方法之猜想与假设

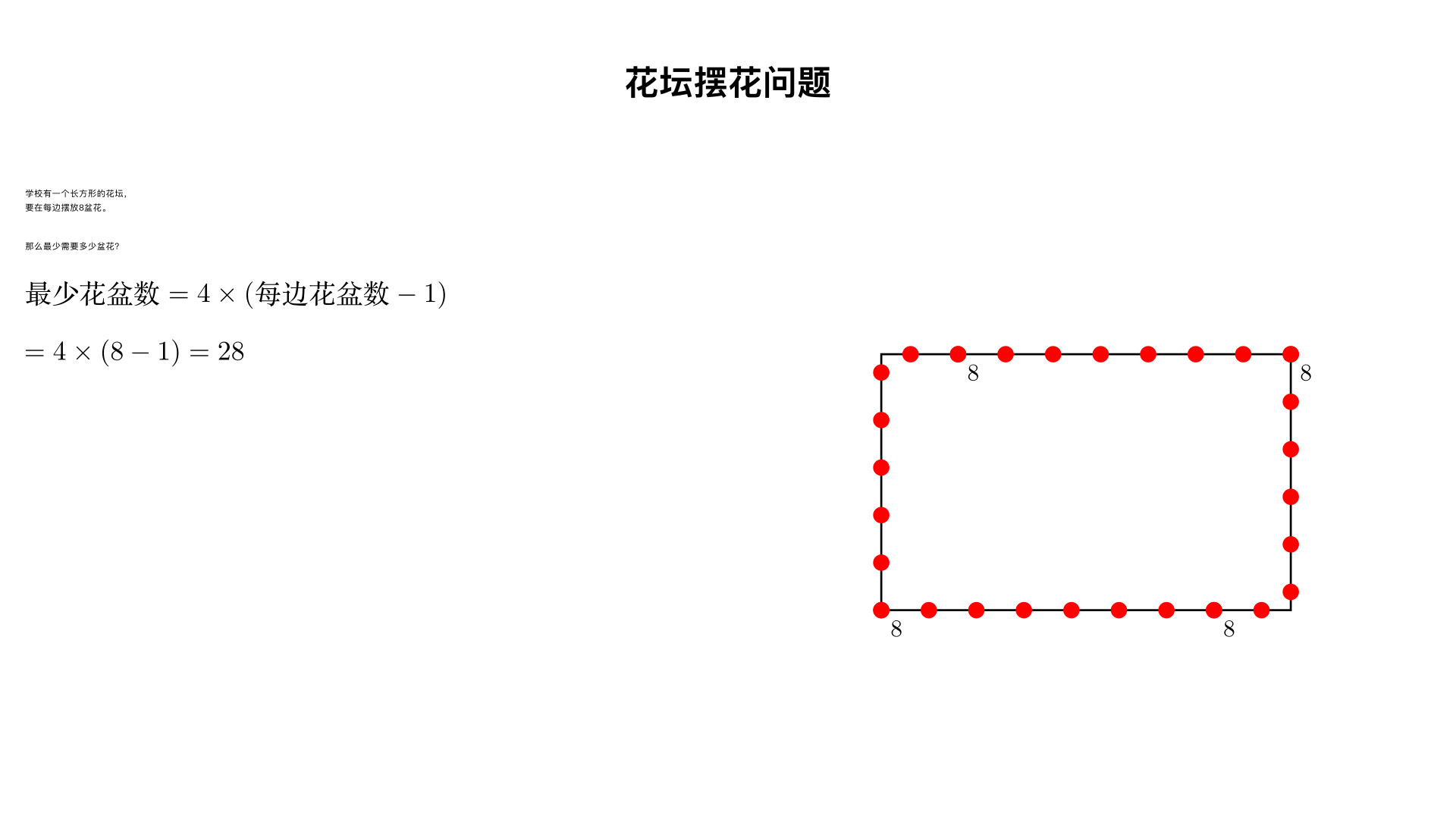
学校有一个长方形的花坛,要在每边摆放8盆花,那么最少需要多少盆花？

小学二年级数学克和千克

人工智能深度学习神经网络基础

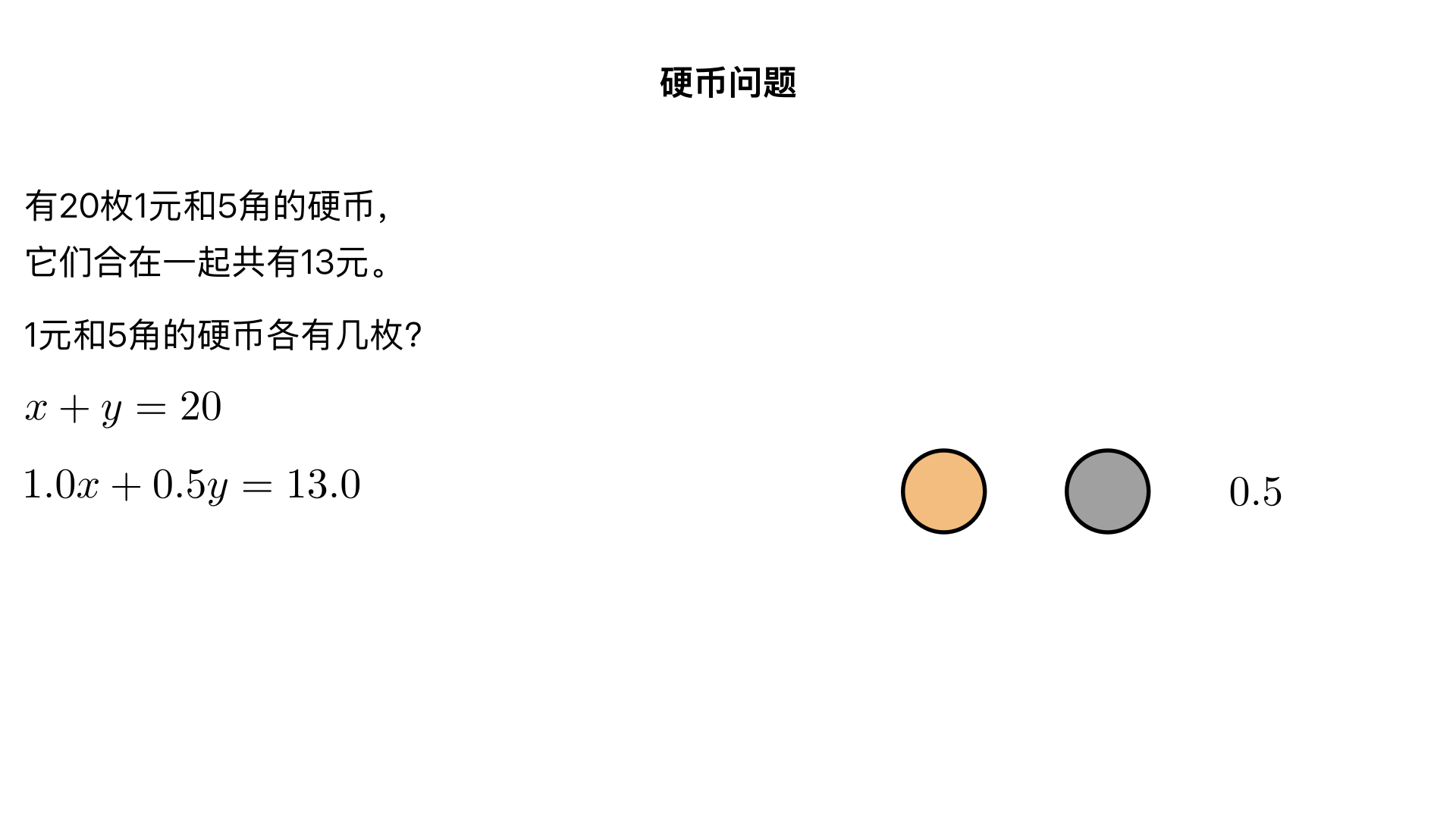
有20枚1元和5角的硬币，它们合在一起共有13元。1元和5角的硬币各有几枚?

妈妈买回一桶油,连桶共重10千克,吃了一半后,连桶重6千克。原来油重多少千克?桶重多少千克?

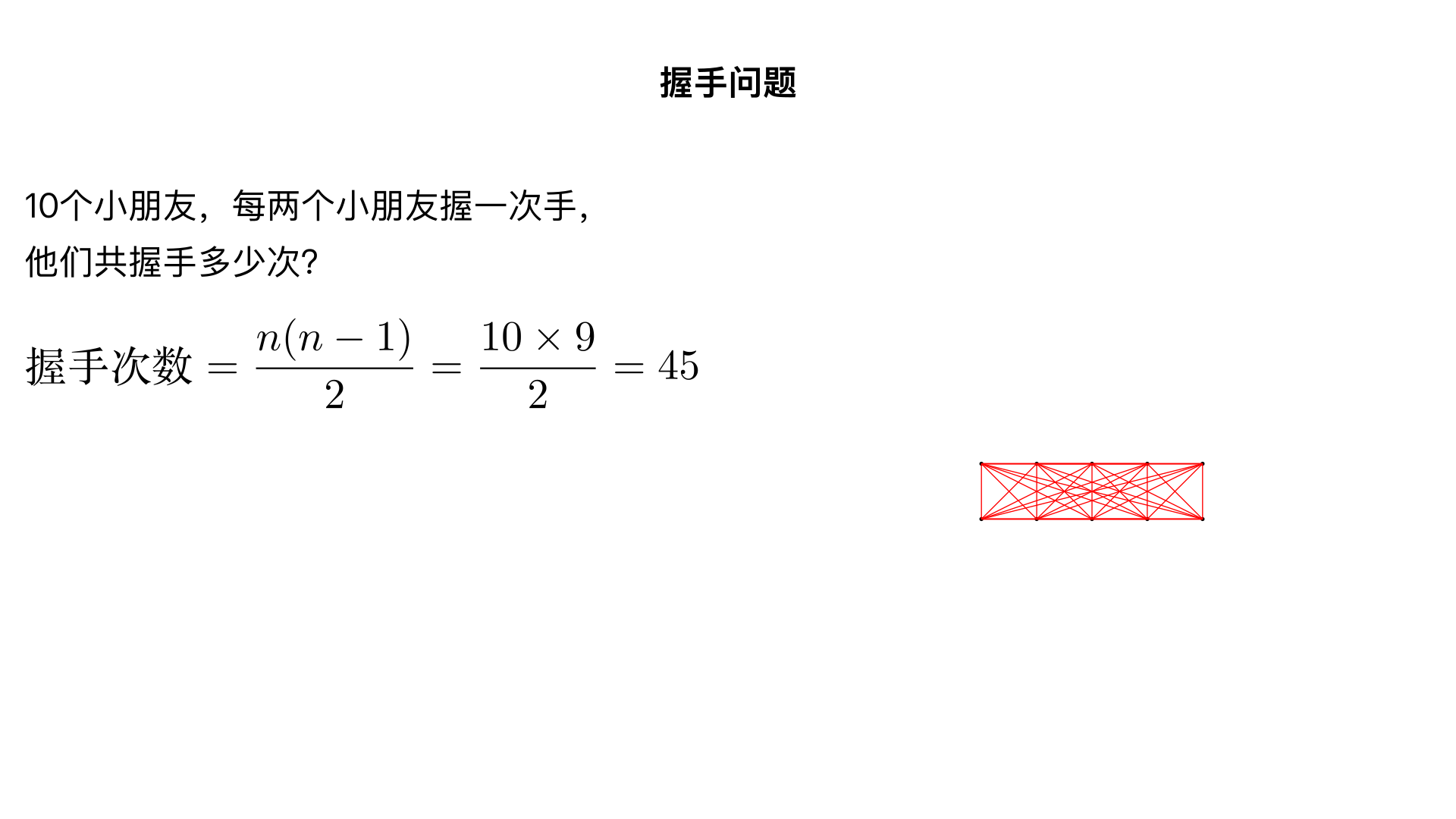
10个小朋友，每两个小朋友握一次手,他们共握手多少次?

鸡和兔共100只，脚共有280只，鸡、免各有几只?

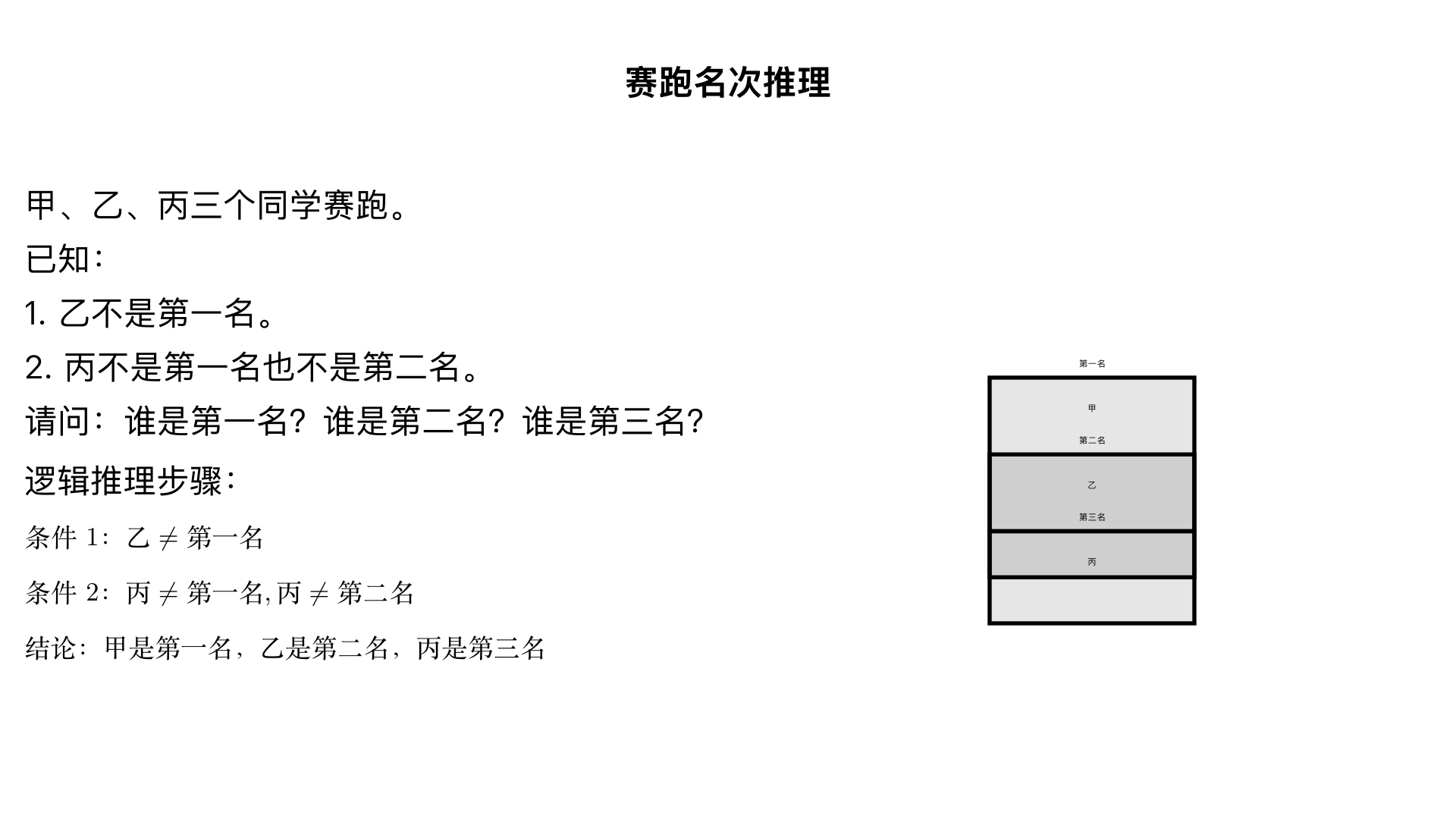
甲、乙、丙三个同学赛跑,已知乙不是第一名,丙不是第一名也不是第二名。谁是第一名?谁是第二名?谁是第三名?