T
Teach Me AnythingTMA
Video History
Page 1 / 126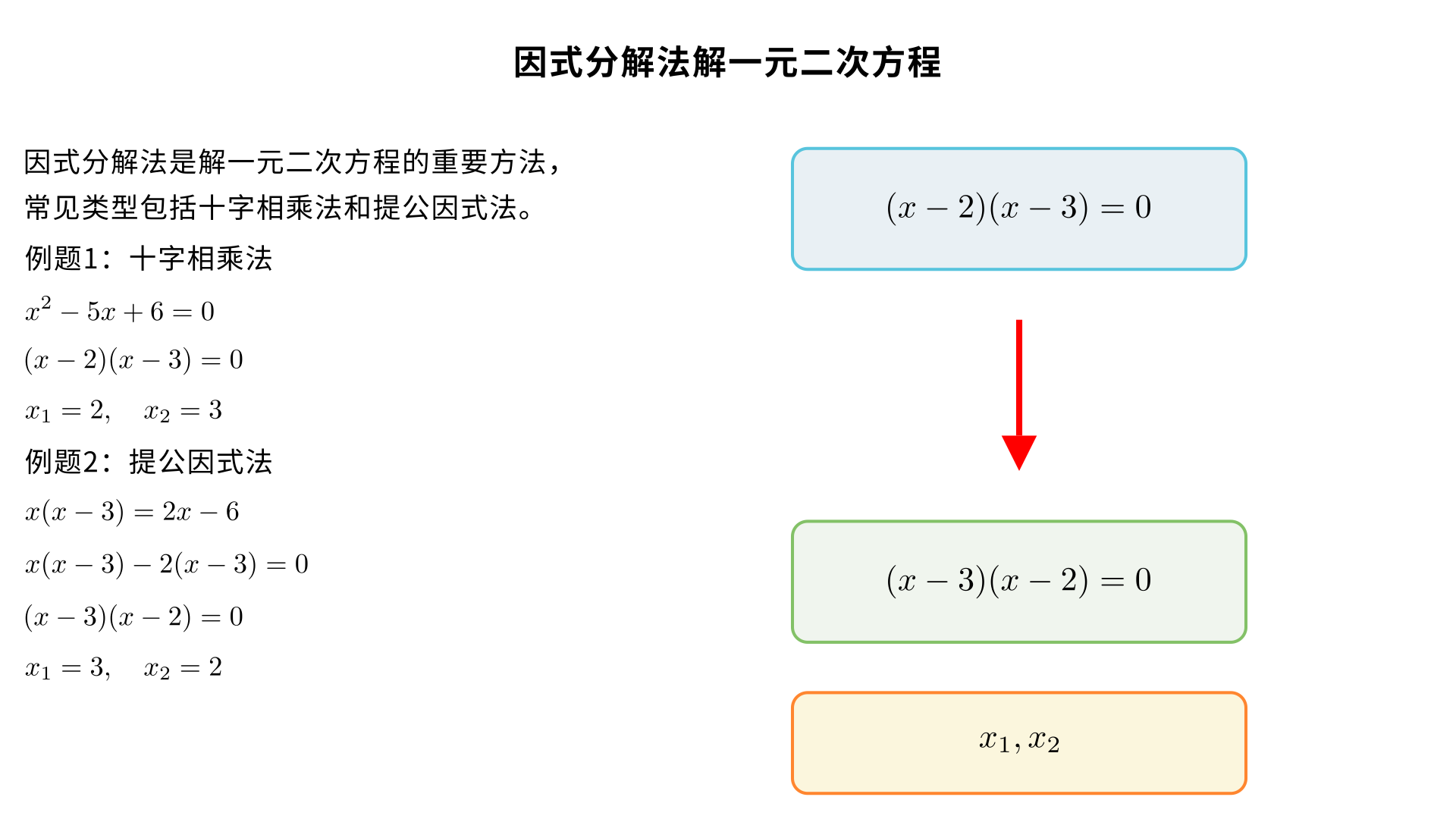
▶
因式分解法 2 道典型考题 例题 1(十字相乘法・最常考) 解方程: x 2 −5x+6=0 解: 左边十字相乘分解 (x−2)(x−3)=0 令每个因式等于 0 x−2=0或x−3=0 得解 x 1 =2, x 2 =3 例题 2(提公因式法・易错题) 解方程: x(x−3)=2x−6 解: 移项,右边化为 0 x(x−3)−2x+6=0 提公因式 x(x−3)−2(x−3)=0 (x−3)(x−2)=0 令每个因式等于 0 x−3=0或x−2=0 得解 x 1 =3, x 2 =2
▶
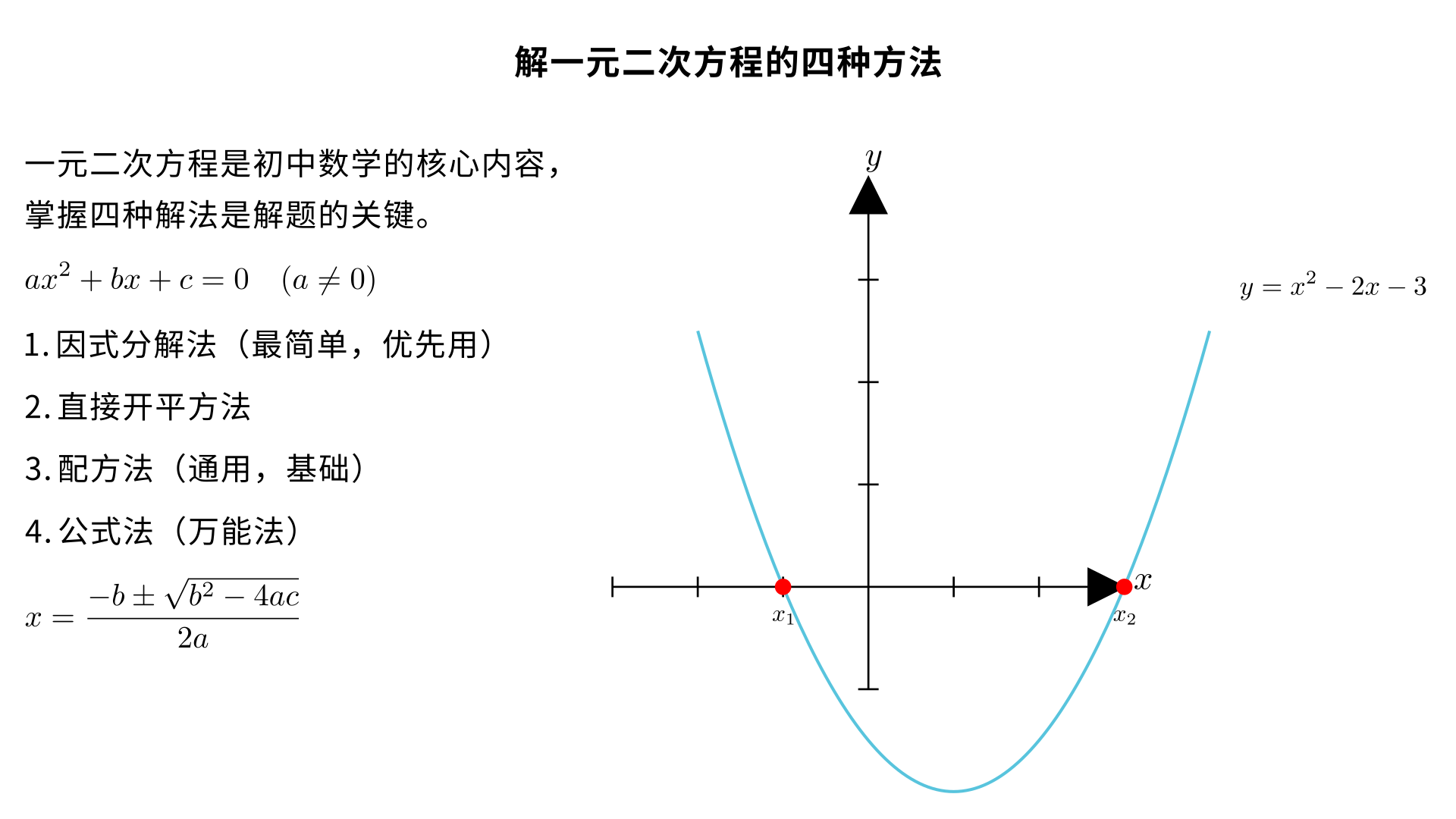
九年级数学:解一元二次方程(核心 4 种方法) 一元二次方程标准形式: , 、 、 为 常 数 按优先使用顺序,共 4 种解法: 一、因式分解法(最简单,优先用) 适用:方程能化成 “两个一次式相乘 = 0”步骤: 移项,使右边 = 0 左边因式分解(提公因式 / 十字相乘) 令每个因式 = 0,解一元一次方程 例: x 2 −5x+6=0 解: (x−2)(x−3)=0 , 二、直接开平方法 适用:形如 (x+m) 2 =n (n≥0) 步骤:两边直接开平方 例: (x−1) 2 =4 解: x−1=±2 , 三、配方法(通用,基础) 步骤: 化二次项系数为 1 移项:常数项移到右边 配方:两边加一次项系数一半的平方 开平方求解 例: x 2 −6x−7=0 解: x 2 −6x=7 x 2 −6x+9=7+9 (x−3) 2 =16 x−3=±4 , 四、公式法(万能法) 先写求根公式: x= 2a −b± b 2 −4ac 判别式: Δ=b 2 −4ac Δ>0 :两个不相等实数根 Δ=0 :两个相等实数根 Δ<0 :无实数根 例: 2x 2 −3x−1=0 , , Δ=9+8=17>0 x= 4 3± 17 解题小口诀 能分解,先分解;平方型,直接开;都不行,用公式;配方法,练基础。
▶
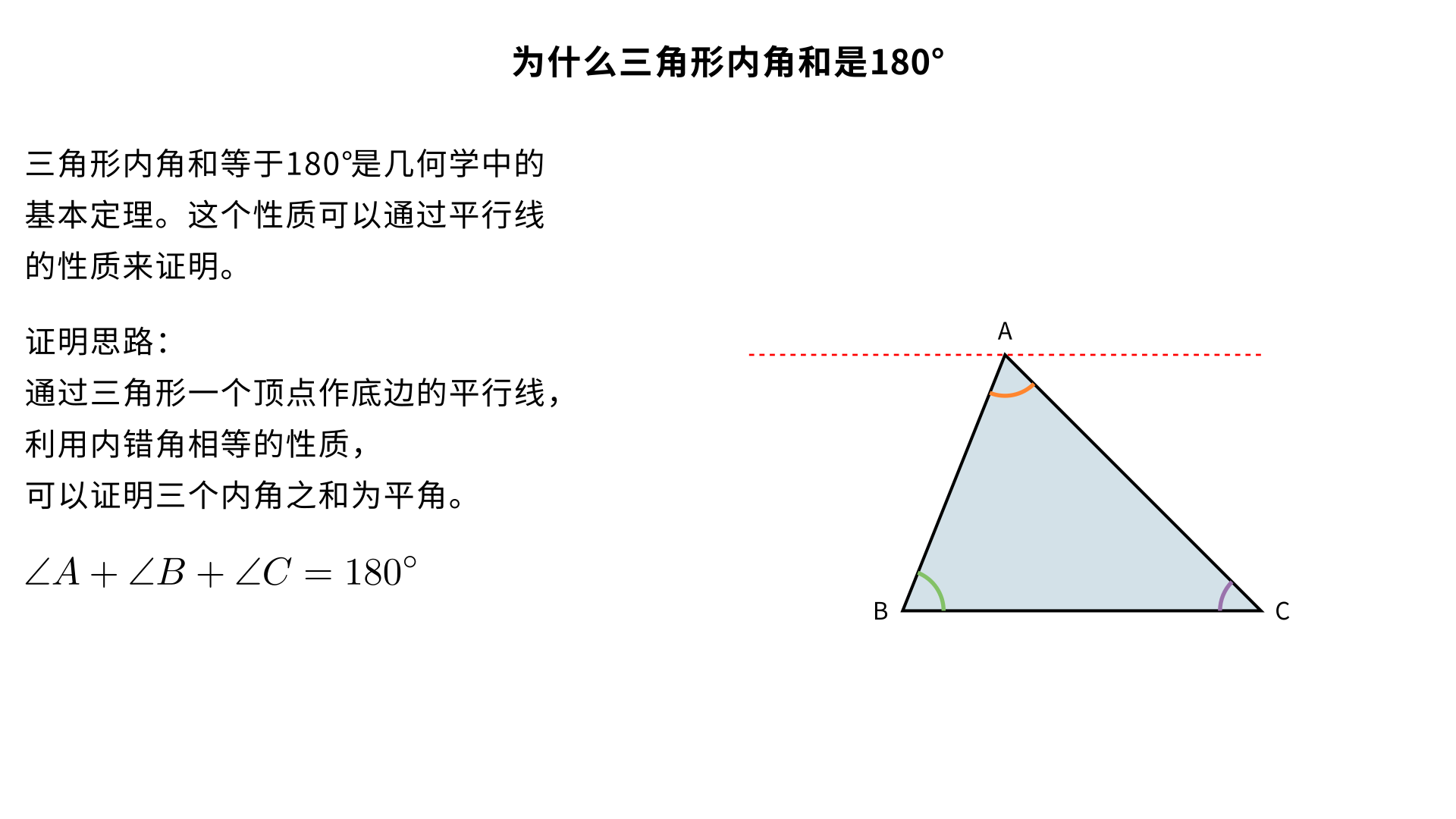
为什么三角形内角和是 180°
▶
max has been listening to our converstation again. He needs to stop. 解释这个句子
▶
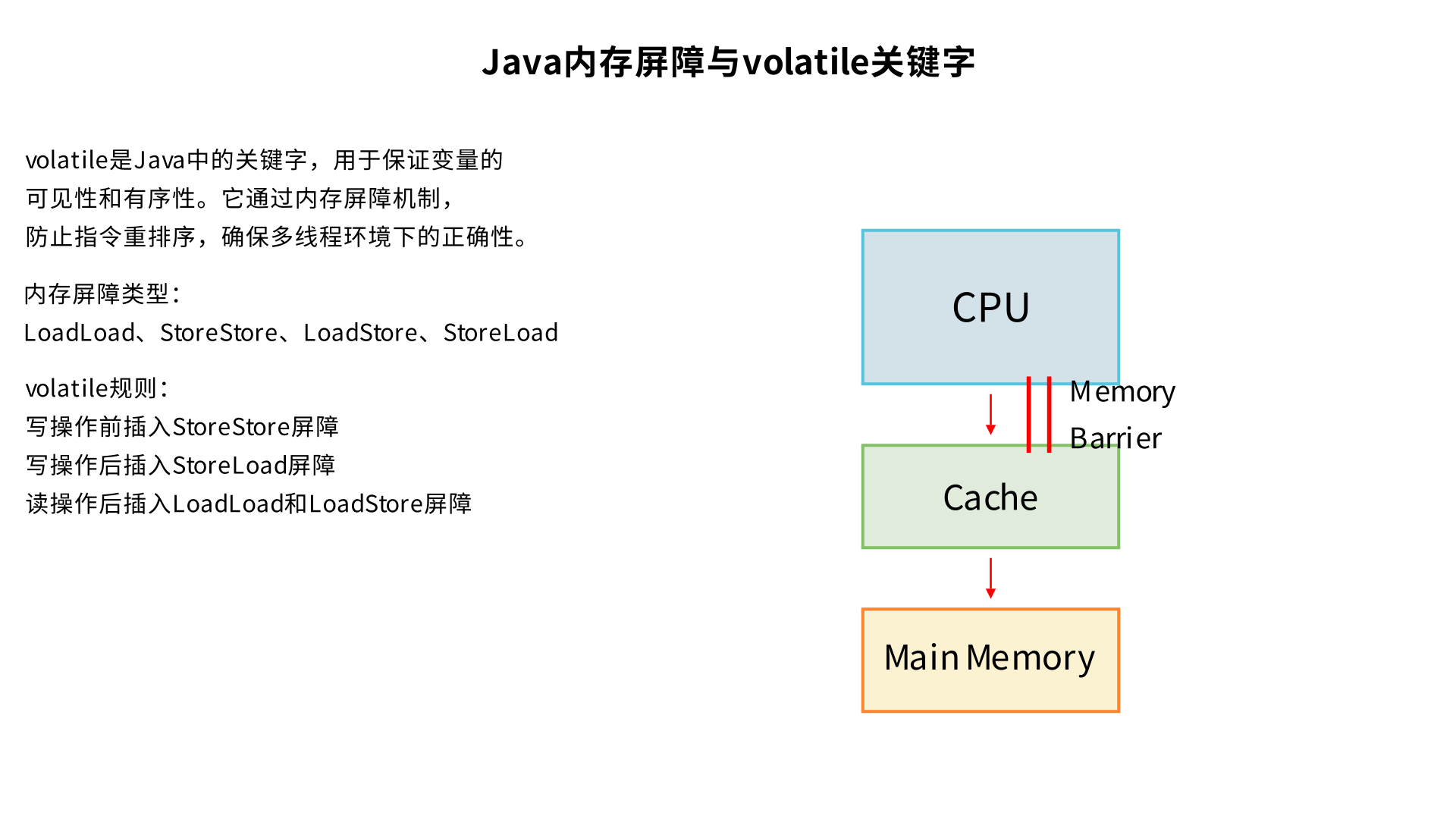
java 内存屏障 volatile 讲解
▶
讲解 宋 王安石的元日
▶
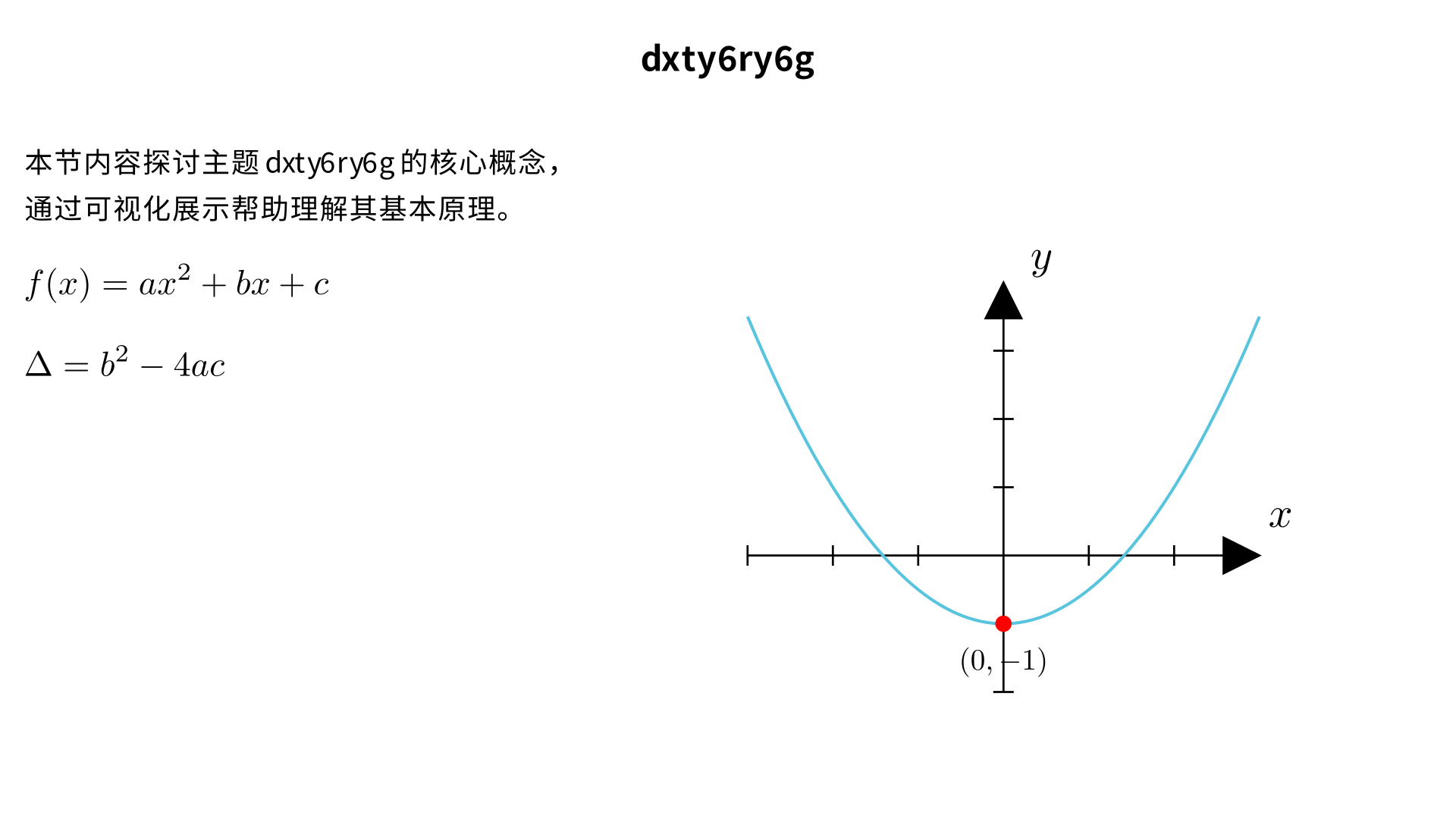
dxty6ry6g
▶
如何用这几个keyword: Antarctica, ice, covered来做一个sentence
▶
如何用这几个keyword: Antarctica, ice, covered来做一个sentence; use english pure

▶
如何用这几个keyword: Antarctica, ice, covered来做一个sentence

▶
如何用这几个keyword: Antarctica, ice, covered来做一个sentence
▶