T
Teach Me AnythingTMA
Video History
Page 12 / 126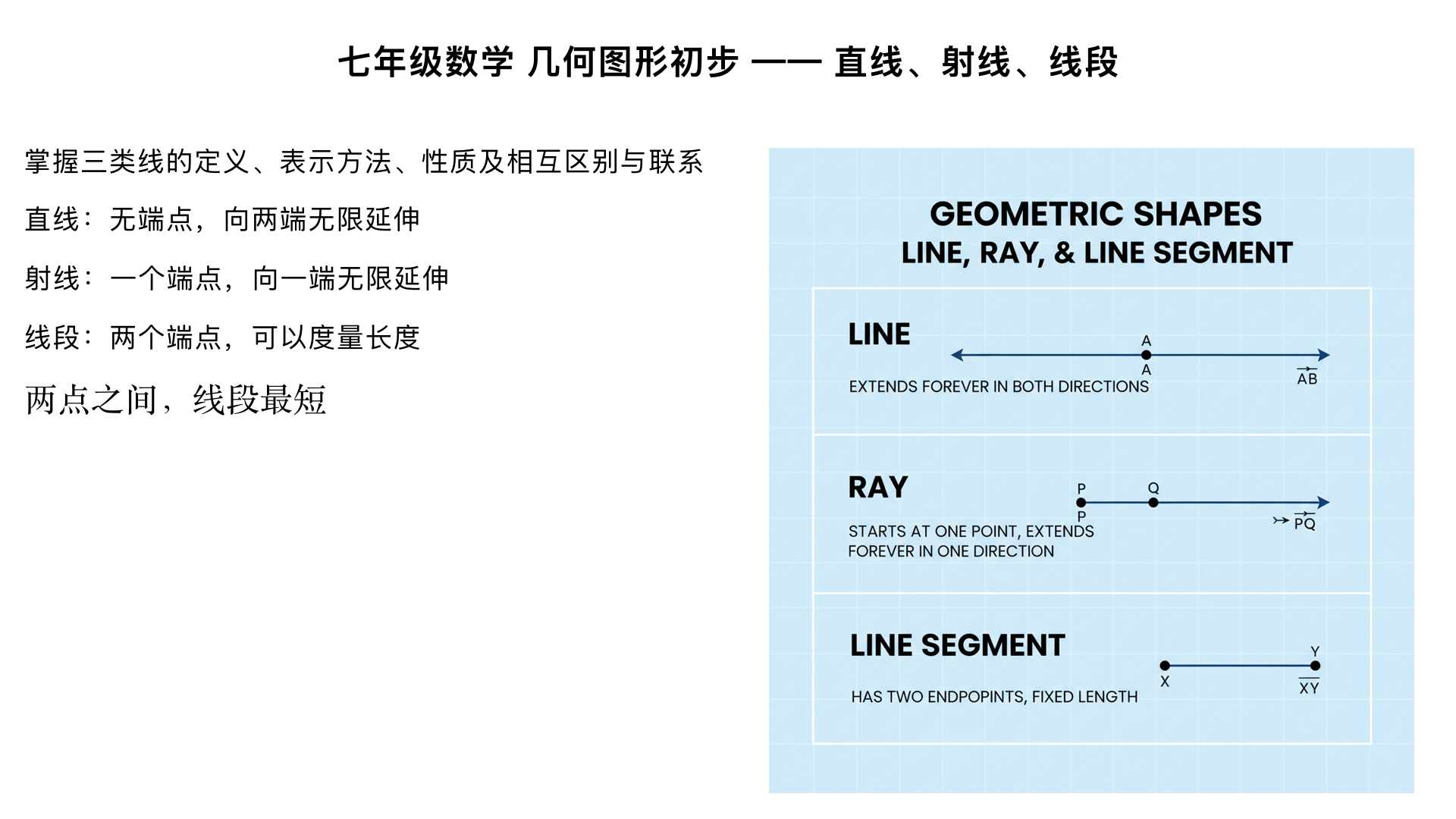
▶
七年级数学 几何图形初步 —— 直线、射线、线段 本小节是几何图形的基础内容,是后续学习角、三角形、四边形等复杂几何图形的前提,核心是掌握三类线的定义、表示方法、性质及相互区别与联系。 一、核心知识点梳理 1. 直线 定义:把线段向两端无限延伸所形成的图形叫做直线,直线没有端点,无法度量长度。 表示方法 用直线上两个点的大写字母表示,如直线 AB (也可写作直线 BA ,字母顺序不影响); 用一个小写字母表示,如直线 l 。 基本性质:两点确定一条直线。 实例:生活中钉木条时,钉两个钉子就能固定木条,就是利用了这一性质。 2. 射线 定义:把线段向一端无限延伸所形成的图形叫做射线,射线有且只有一个端点,无法度量长度。 表示方法:用端点字母和射线上另一个点的大写字母表示,端点字母必须写在前面,如射线 OA (不能写作射线 AO ,因为端点不同,射线的延伸方向也不同);也可单独用一个小写字母表示,如射线 m 。 特点:有一个端点,向一端无限延伸,同一端点、不同延伸方向的射线是不同的射线。 3. 线段 定义:直线上两个点和它们之间的部分叫做线段,线段有两个端点,能够度量长度。 表示方法 用线段的两个端点的大写字母表示,如线段 AB (也可写作线段 BA ); 用一个小写字母表示,如线段 a 。 基本性质:两点之间,线段最短,两点之间线段的长度叫做这两点之间的距离。 线段的中点:若点 M 把线段 AB 分成相等的两条线段 AM 和 MB ,则点 M 叫做线段 AB 的中点,此时 AM=MB= 2 1 AB 。 二、直线、射线、线段的区别与联系 图形 端点个数 延伸性 能否度量长度 表示方法(示例) 直线 0 个 向两端无限延伸 不能 直线 AB 、直线 l 射线 1 个 向一端无限延伸 不能 射线 OA 、射线 m 线段 2 个 不能延伸(可延长) 能 线段 AB 、线段 a 联系:射线和线段都是直线的一部分;将射线反向延伸、将线段向两端延伸都可得到直线。 三、典型例题解析 例 1 判断下列说法是否正确:(1)直线 AB 和直线 BA 是同一条直线;(2)射线 AB 和射线 BA 是同一条射线;(3)线段 AB 和线段 BA 是同一条线段。 解析(1)正确,直线的表示与字母顺序无关;(2)错误,射线 AB 的端点是 A ,向 B 方向延伸,射线 BA 的端点是 B ,向 A 方向延伸,二者不是同一条射线;(3)正确,线段的表示与字母顺序无关。 例 2 已知线段 AB=8 cm ,点 C 是线段 AB 的中点,求线段 AC 的长度。 解析因为点 C 是 AB 的中点,所以 AC= 2 1 AB ,又 AB=8 cm ,因此 AC=4 cm 。 四、易错点提醒 射线的表示需注意端点字母在前,不能颠倒顺序; 直线和射线无法度量长度,不能说 “画一条长度为 5cm 的直线” 或 “射线 OA 长 3cm”; “两点之间的距离” 指的是线段的长度,不是线段本身。
▶
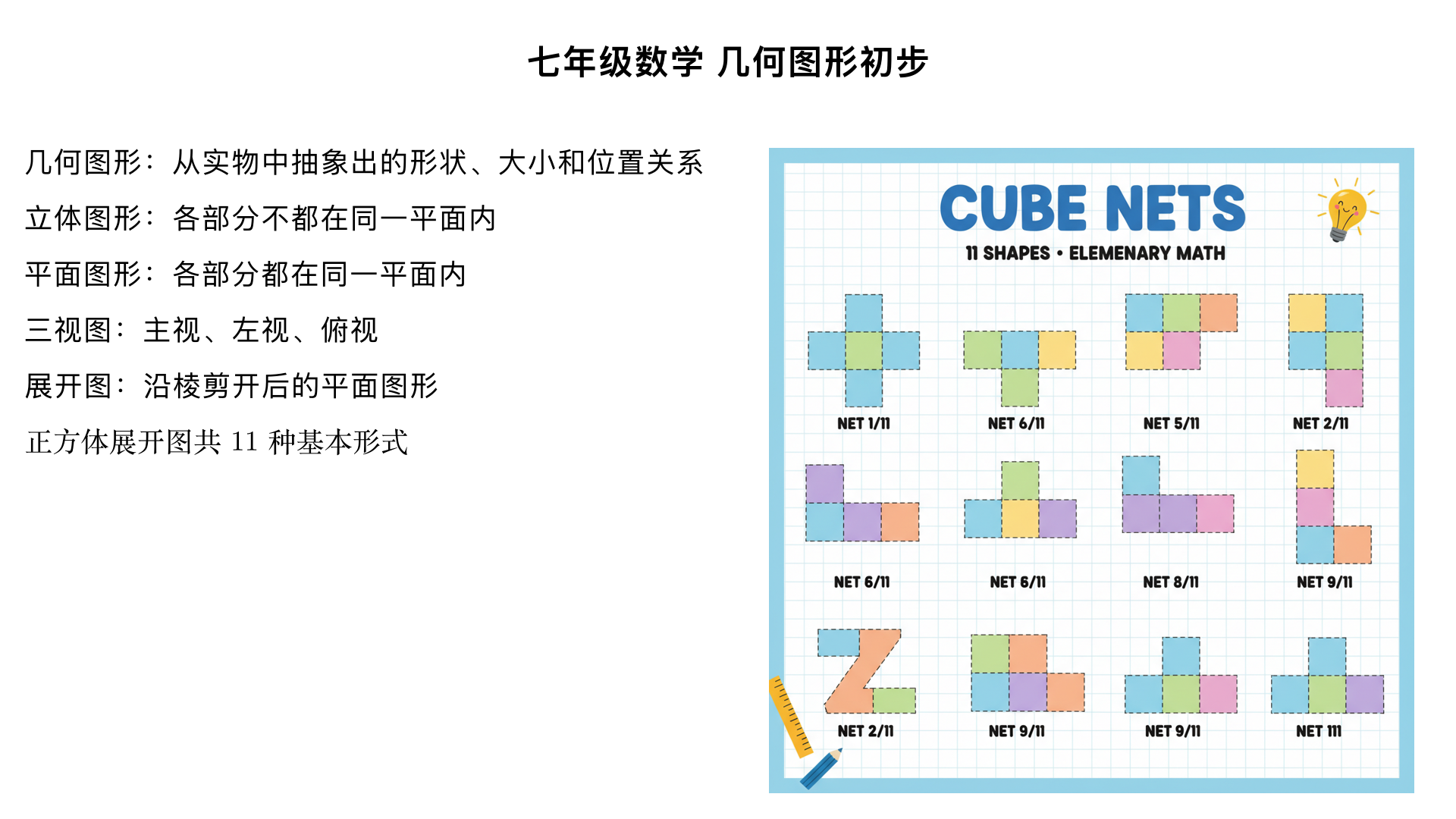
七年级数学 几何图形初步 - 几何图形 知识点梳理 本小节是几何学习的入门内容,核心是认识各类几何图形的特征、区分立体与平面图形,以及掌握立体图形的视图和展开图,为后续几何知识学习奠定基础。 一、几何图形的基本概念 几何图形:从实物中抽象出来的各种图形,统称为几何图形。几何图形只关注物体的形状、大小和位置关系,不考虑颜色、材质等其他属性。 例如:篮球抽象为球体、书本抽象为长方体、三角尺抽象为三角形。 二、立体图形与平面图形 1. 立体图形(几何体) 定义:各部分不都在同一平面内的几何图形,具有一定的空间立体感。常见的立体图形分类及特征如下表: 类别 代表图形 核心特征 柱体 圆柱 有两个大小相等的圆形底面,侧面是曲面,底面与侧面垂直 棱柱(三棱柱、四棱柱等) 有两个全等的多边形底面,侧面是长方形(直棱柱),侧棱平行且相等 锥体 圆锥 有一个圆形底面,一个顶点,侧面是曲面 棱锥(三棱锥、四棱锥等) 有一个多边形底面,侧面是三角形,所有侧面三角形的顶点汇聚于一点 球体 球 整个图形由曲面围成,任意截面为圆形,无顶点和棱 2. 平面图形 定义:各部分都在同一平面内的几何图形。常见平面图形:三角形、正方形、长方形、圆形、五边形、六边形等。 注意:立体图形的某个 “面” 可以是平面图形,例如正方体的每个面都是正方形。 三、从不同方向看立体图形 从不同方向观察立体图形,会得到不同的平面图形,通常从正面、左面、上面三个方向观察,对应的图形分别称为主视图、左视图、俯视图(合称 “三视图”)。 示例:观察正方体,三个视图都是正方形;观察圆柱,主视图和左视图是长方形,俯视图是圆形。 作用:通过三视图可完整还原立体图形的形状,是工程制图、建筑设计的基础。 四、立体图形的展开图 定义:将立体图形的表面沿棱剪开,展开后得到的平面图形,称为该立体图形的展开图。 常见立体图形的展开图特征 正方体展开图:由 6 个正方形组成,共有 11 种基本形式,无 “田” 字格、“凹” 字形结构。 圆柱展开图:由 2 个圆形(上下底面)和 1 个长方形(侧面)组成,长方形的长等于底面圆的周长。 圆锥展开图:由 1 个圆形(底面)和 1 个扇形(侧面)组成,扇形的弧长等于底面圆的周长。 注意事项:不是所有平面图形都能折叠成对应立体图形,需结合立体图形的棱、面数量和位置判断。
▶
统筹规划:给一块小木板两面刷油漆,每刷一面要1分钟,但必须要等5分钟油漆干了后才能给另一面刷油漆。那么要尽快刷完6块这样的小木板共需多少分钟? 一、题型判断:统筹规划问题(小学奥数 “时间优化” 子类) 这类题型的核心是通过合理安排操作顺序,最大化利用等待时间(如油漆干燥时间),避免无效等待,从而缩短总耗时。解题关键是 “并行操作”—— 在等待前一步操作完成(如油漆干燥)的同时,进行其他相关操作,本质是 “时间资源的最优分配”。 二、解题过程(分步骤拆解:明确操作规则→设计最优流程→计算总时间) 已知条件: 1 块木板需刷 2 面,每面刷漆耗时 1 分钟; 刷完一面后,需等 5 分钟油漆干燥才能刷另一面; 共 6 块木板,目标:尽快刷完,最短化总时间。 关键逻辑:避免单块木板 “刷完一面后空等 5 分钟” 如果逐块刷(刷完 A1 面→等 5 分钟→刷 A2 面→再刷 B1 面→等 5 分钟→刷 B2 面…),总时间会很长(6×(1+5+1)=42 分钟)。最优策略:刷完一块木板的第一面后,立刻刷下一块木板的第一面,利用后续木板的刷漆时间覆盖前一块的干燥时间,待所有木板第一面刷完后,前几块木板的油漆已干燥,可直接刷第二面。 具体流程(以 6 块木板记为①-⑥为例) 第一步:刷所有木板的第一面(并行利用干燥时间) 第 1 分钟:刷①的正面(①正); 第 2 分钟:刷②的正面(②正); 第 3 分钟:刷③的正面(③正); 第 4 分钟:刷④的正面(④正); 第 5 分钟:刷⑤的正面(⑤正); 第 6 分钟:刷⑥的正面(⑥正);此时,所有木板第一面刷完,耗时 6 分钟。关键:刷完①正后,无需等待,直接刷②正,①正的干燥时间从第 1 分钟结束开始计算,到第 6 分钟结束时,①正已干燥了 5 分钟(满足 “干燥 5 分钟” 的要求),②正干燥了 4 分钟,③正干燥了 3 分钟,④正干燥了 2 分钟,⑤正干燥了 1 分钟,⑥正刚刷完(干燥 0 分钟)。 第二步:刷所有木板的第二面(按干燥顺序刷,无等待) 第 7 分钟:刷①的反面(①反)(①正已干燥 5 分钟,符合要求); 第 8 分钟:刷②的反面(②反)(②正已干燥 5 分钟,符合要求); 第 9 分钟:刷③的反面(③反)(③正已干燥 5 分钟,符合要求); 第 10 分钟:刷④的反面(④反)(④正已干燥 5 分钟,符合要求); 第 11 分钟:刷⑤的反面(⑤反)(⑤正已干燥 5 分钟,符合要求); 第 12 分钟:刷⑥的反面(⑥反)(⑥正从第 6 分钟结束开始干燥,到第 12 分钟结束时已干燥 6 分钟,满足要求); 总时间计算 第一步 6 分钟 + 第二步 6 分钟 = 12 分钟。 三、反推验证(确认流程合理性,无无效等待) 干燥时间验证: ①正刷完时间(第 1 分钟结束)→ ①反刷完时间(第 7 分钟开始),间隔 6 分钟≥5 分钟,干燥充分 ✔️; ②正刷完时间(第 2 分钟结束)→ ②反刷完时间(第 8 分钟开始),间隔 6 分钟≥5 分钟,干燥充分 ✔️; 以此类推,⑥正刷完时间(第 6 分钟结束)→ ⑥反刷完时间(第 12 分钟开始),间隔 6 分钟≥5 分钟,干燥充分 ✔️; 操作连续性验证:整个流程无空等时间,刷漆操作连续进行(第 1-12 分钟均在刷漆,无停顿),最大化利用时间 ✔️; 极限验证:若减少木板数量(如 2 块),按此流程:刷 2 面正面(2 分钟)→ 刷 2 面反面(2 分钟),总时间 4 分钟(刷①正→②正→①反→②反,①正干燥 2 分钟?不,2 块木板时:第 1 分钟①正,第 2 分钟②正,第 3 分钟①反(①正干燥 2 分钟<5 分钟,需等 3 分钟到第 5 分钟再刷①反,总时间 5+2=7 分钟),但 6 块木板时,刷完 6 面正面刚好耗时 6 分钟,前 5 块木板的干燥时间已满足,无需额外等待,是最优情况 ✔️。 四、最终结果 尽快刷完 6 块小木板共需 12 分钟。
▶
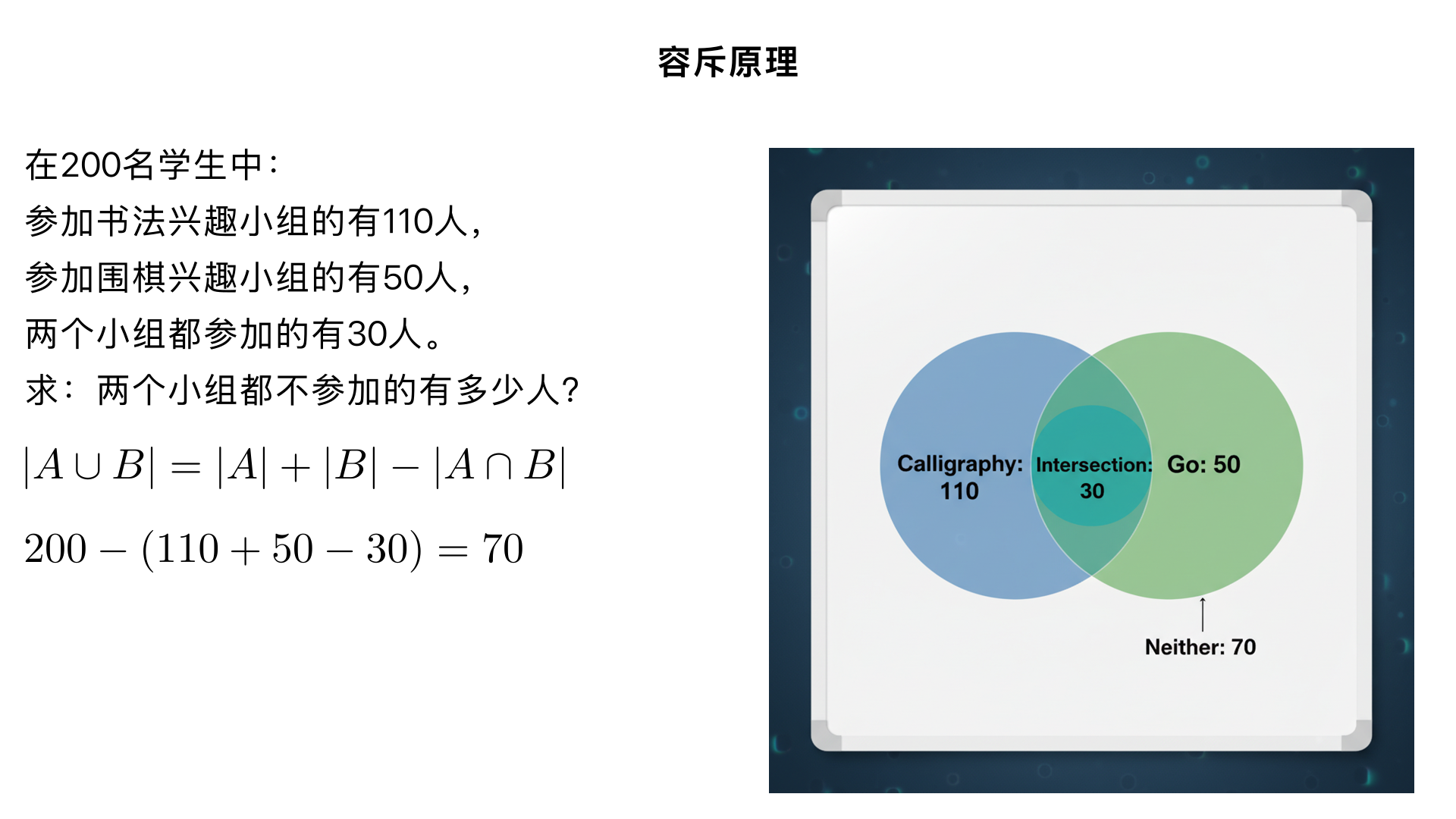
容斥原理:在200名学生中,参加书法兴趣小组的有110人,参加围棋兴趣小组的有50人,其中两个小组都参加的有30人,那么两个小组都不参加的有多少人? 一、题型判断:容斥原理问题(小学奥数 “两集合容斥原理” 子类) 这类题型的核心是通过 “总人数、两个集合的单独人数、两集合重叠人数”,推导 “两个集合都不参与的人数” 。解题关键是先利用容斥原理求出 “至少参加一个小组的人数”,再用总人数减去该数值,本质是 “集合重叠部分的反向计算应用”。 二、解题过程(分 2 步:求至少参加一个小组的人数→求都不参加的人数) 已知条件: 总人数 = 200 人; 参加书法小组(A)=110 人,参加围棋小组(B)=50 人; 两个小组都参加的人数(A∩B)=30 人; 求:两个小组都不参加的人数(记为 y)。 核心逻辑:总人数 = 至少参加一个小组的人数 + 都不参加的人数,因此先通过容斥原理求 “至少参加一个小组的人数”,再反向求 y。 步骤 1:计算至少参加一个兴趣小组的人数 两集合容斥原理核心公式(避免重复计算重叠部分):至少参加一个小组的人数 = 参加书法的人数 + 参加围棋的人数 - 两个小组都参加的人数代入数据:110 + 50 - 30 = 130 人。 步骤 2:计算两个小组都不参加的人数 根据总人数的构成关系:都不参加的人数 = 总人数 - 至少参加一个小组的人数代入数据:y = 200 - 130 = 70 人。 三、反推验证(核对所有条件,逻辑闭环) 至少参加一个小组的人数验证:110(书法)+50(围棋)-30(同时参加)=130 人,重叠部分未重复计算,逻辑正确 ✔️; 总人数验证:130(至少参加一个)+70(都不参加)=200 人,与题目总人数一致 ✔️; 细分人数验证:只参加书法的人数 = 110-30=80 人,只参加围棋的人数 = 50-30=20 人,同时参加的 30 人,都不参加的 70 人,80+20+30+70=200 人,无重复、无遗漏 ✔️。 四、最终结果 两个小组都不参加的有 70 人。

▶
容斥原理在1到100的全部自然数中,既不是8的倍数也不是5的倍数的数有多少个? 一、题型判断:容斥原理问题(小学奥数 “两集合容斥原理 + 数的倍数” 子类) 这类题型的核心是先找出 “1 到 100 中是 8 的倍数或 5 的倍数的数的总个数”,再用总数减去这个数,得到 “既不是 8 的倍数也不是 5 的倍数的数的个数” 。解题关键是利用容斥原理避免重复计算 “既是 8 的倍数又是 5 的倍数” 的数,本质是 “集合重叠思想在数的倍数问题中的应用”。 二、解题过程(分 4 步:找倍数个数→算重叠个数→求符合条件的倍数总数→求目标个数) 已知条件: 范围:1 到 100 的全部自然数(总个数 = 100 个); 核心问题:求 “既不是 8 的倍数也不是 5 的倍数” 的数的个数; 解题逻辑:总个数 - (是 8 的倍数的数的个数 + 是 5 的倍数的数的个数 - 既是 8 又是 5 的倍数的数的个数)= 目标个数(避免重复计算重叠部分)。 步骤 1:计算 1 到 100 中是 8 的倍数的数的个数(记为 A) 用 “去尾法” 计算(只取整数部分,不四舍五入):100÷8=12.5 → 取整数 12 个(分别是 8、16、24、…、96);即 A=12。 步骤 2:计算 1 到 100 中是 5 的倍数的数的个数(记为 B) 同理,100÷5=20 → 刚好是整数,共 20 个(分别是 5、10、15、…、100);即 B=20。 步骤 3:计算 1 到 100 中既是 8 的倍数又是 5 的倍数的数的个数(记为 A∩B,即重叠个数) 既是 8 的倍数又是 5 的倍数,说明是 8 和 5 的最小公倍数的倍数;8 和 5 互质,最小公倍数 = 8×5=40;因此,只需计算 1 到 100 中是 40 的倍数的数的个数:100÷40=2.5 → 取整数 2 个(分别是 40、80);即 A∩B=2。 步骤 4:计算 “既不是 8 的倍数也不是 5 的倍数” 的数的个数 根据容斥原理,先求 “是 8 的倍数或 5 的倍数” 的数的总个数:A + B - A∩B=12+20-2=30 个;再用 1 到 100 的总个数减去这个数,得到目标个数:100 - 30=70 个。 三、反推验证(核对所有计算,逻辑闭环) 倍数个数验证: 8 的倍数有 12 个(8×1 到 8×12),5 的倍数有 20 个(5×1 到 5×20),重叠的 40 的倍数有 2 个(40×1、40×2),无遗漏、无重复 ✔️; “是 8 或 5 的倍数” 的总数验证:12+20-2=30 个,计算正确 ✔️; 目标个数验证:100(总个数)-30(是 8 或 5 的倍数的个数)=70 个,反向核对:若既不是 8 也不是 5 的倍数有 70 个,加上 30 个符合倍数条件的数,总数 = 70+30=100,与 1 到 100 的自然数总数一致 ✔️; 实例验证:随机抽取 1-10 的数,既不是 8 也不是 5 的倍数的有 1、2、3、4、6、7、9,共 7 个;用公式计算 1-10 中:8 的倍数 1 个(8),5 的倍数 1 个(5),重叠 0 个,总数 10-(1+1-0)=8?不对,1-10 中既不是 8 也不是 5 的倍数的是 1、2、3、4、6、7、9,共 7 个,哦,遗漏了 10 是 5 的倍数,所以 1-10 中符合倍数条件的是 5、8、10,共 3 个,10-3=7,与公式计算(1+2-0=3,10-3=7)一致,说明公式应用正确 ✔️。 四、最终结果 在 1 到 100 的全部自然数中,既不是 8 的倍数也不是 5 的倍数的数有 70 个。

▶
容斥原理:某班有68人,参加足球兴趣小组的有32人,参加排球兴趣小组的有30人,如果两个兴趣小组都没有参加的有25人,那么同时参加足球、排球两个兴趣小组的有多少人? 一、题型判断:容斥原理问题(小学奥数 “两集合容斥原理” 子类) 这类题型的核心是解决两个集合的重叠部分计算,通过 “总人数、未参与人数、两个集合单独参与人数” 的关系,推导同时属于两个集合的人数。解题关键是先明确 “至少参与一个集合的人数”,再利用 “两集合总和 - 重叠人数 = 至少参与一个集合的人数” 的逻辑,本质是 “避免重复计算重叠部分”。 二、解题过程(分 2 步:求参与总人数→求重叠人数) 已知条件: 全班总人数 = 68 人; 两个小组都未参加的人数 = 25 人; 参加足球小组(A)= 32 人,参加排球小组(B)= 30 人; 求:同时参加两个小组的人数(记为 x)。 核心逻辑:先算出 “至少参加一个兴趣小组的人数”,再用两集合容斥原理公式反向求重叠人数。 步骤 1:计算至少参加一个兴趣小组的人数 总人数由 “至少参加一个小组的人” 和 “都未参加的人” 组成,因此:至少参加一个小组的人数 = 总人数 - 都未参加的人数= 68 - 25 = 43 人。 步骤 2:用容斥原理公式求重叠人数 x 两集合容斥原理核心公式(避免重复计算):参加足球的人数 + 参加排球的人数 - 同时参加的人数 = 至少参加一个小组的人数代入数据列等式:32 + 30 - x = 43 化简计算:62 - x = 43x = 62 - 43 = 19 人。 三、反推验证(核对所有条件,逻辑闭环) 重叠人数验证:参加足球和排球的总人数为 32+30=62 人,其中重叠部分被多算了 1 次,减去重叠人数 19 人,得到实际参与至少一个小组的人数 = 62-19=43 人 ✔️; 总人数验证:至少参与一个小组的 43 人 + 都未参与的 25 人 = 68 人,与全班总人数一致 ✔️; 细分人数验证:只参加足球的人数 = 32-19=13 人,只参加排球的人数 = 30-19=11 人,同时参加的 19 人,都未参加的 25 人,13+11+19+25=68 人,无重复、无遗漏 ✔️。 四、最终结果 同时参加足球、排球两个兴趣小组的有 19 人。
▶
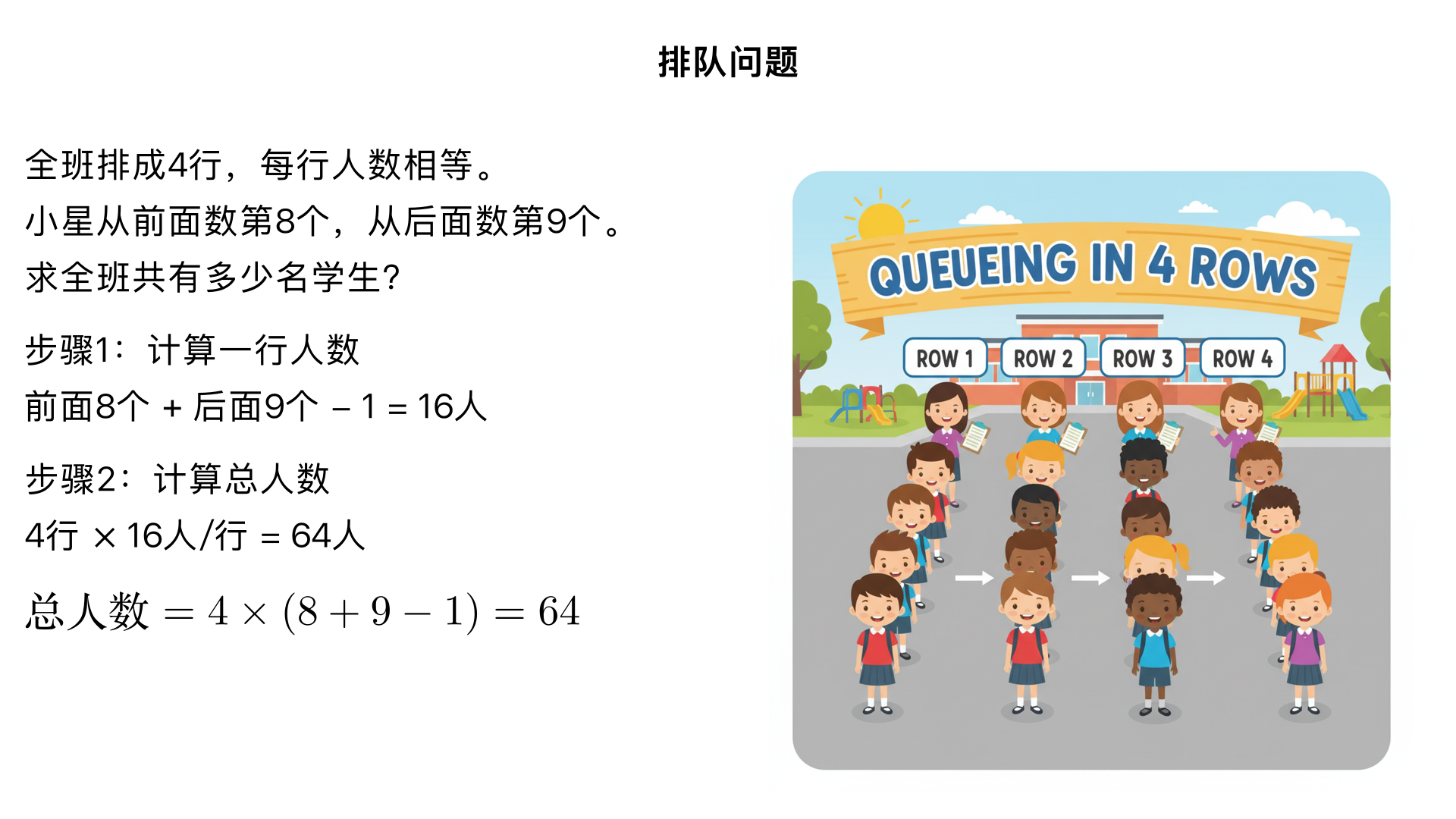
排队问题:某班学生排队,全班排成4行,每行的人数相等,小星排的位置是:从前面数第8个,从后面数第9个,这个班共有多少名学生? 一、题型判断:排队问题(小学奥数 “队列人数计算” 子类) 这类题型的核心是通过 “某个人的前后位置” 求出一行的人数,再结合行数计算总人数。解题关键是避免 “重复计算本人”,即前后位置数相加后需减 1,本质是 “线性队列中单个位置与总行数的关系应用”。 二、解题过程(分 2 步:求一行的人数→求全班总人数) 已知条件: 全班排成 4 行,每行人数相等(均匀分布); 小星的位置:从前面数第 8 个,从后面数第 9 个; 核心逻辑:先算一行的人数(前后位置数相加减 1,避免重复算小星),再乘行数得总人数。 步骤 1:计算一行的人数 从前面数小星是第 8 个,说明小星前面有 7 人;从后面数是第 9 个,说明小星后面有 8 人。一行的人数 = 前面的人数 + 小星本人 + 后面的人数 = 7+1+8=16 人;或用简便公式:一行人数 = 前面位置数 + 后面位置数 - 1(减去重复计算的小星),即 8+9-1=16 人。 步骤 2:计算全班总人数 全班共 4 行,每行 16 人,总人数 = 行数 × 每行人数 = 4×16=64 人。 三、反推验证(核对位置逻辑和总人数,确认一致) 一行人数验证:8(前数位置)+9(后数位置)-1=16 人,避免了 “小星被重复计算”,逻辑正确 ✔️; 总人数验证:4 行 ×16 人 / 行 = 64 人,符合 “每行人数相等” 的条件 ✔️; 位置还原验证:一行 16 人,小星从前面数第 8 个,后面还有 16-8=8 人,因此从后面数是第 8+1=9 个,与题目条件完全一致 ✔️。 四、最终结果 这个班共有 64 名 学生。
▶
噬嗑、贲、剥、复——法治、文饰与阴阳消长 一、噬嗑卦(火雷噬嗑)的法治精神 1. 卦象的直观象征 上离下震:电闪雷鸣,象征刑罚 卦形象如口中含物:需咬合(惩治)方能亨通 2. 《彖传》精讲 “颐中有物曰噬嗑”:如口中含物需咬碎 “刚柔分动而明”:卦中阴阳爻相间,离明震动 “雷电合而章”:雷电交加彰明刑罚 金景芳重点:这是《周易》中论述法治的核心卦 3. 爻辞的刑罚等级 初九、六二、六三:惩治小恶(屦校灭趾、噬肤灭鼻) 九四:“噬干胏,得金矢”**:处理难案需刚直(金矢象征刚直) 六五:“噬干肉,得黄金”**:君主用刑需适中(黄金象征中道) 上九:“何校灭耳”**:积恶不改,终受重刑 二、贲卦(山火贲)的文饰之道 1. 与噬嗑的对比 噬嗑后需贲:法治之后需文教 上艮下离:山下有火,文明照亮山体(文饰) 2. 文饰的辩证法 初九:“贲其趾,舍车而徒”:质朴胜过装饰 六二:“贲其须”:必要的修饰(如胡须修饰脸面) 上九:“白贲,无咎”:回归素白,最高境界 金景芳重点:由文返质,“绚烂之极归于平淡”的哲学 三、剥卦(山地剥)的阴盛阳衰 1. 卦象的危机感 上艮下坤:山附于地,剥落之象 五阴剥一阳:象征小人道长,君子道消 2. 爻辞的剥落过程 从初六到六四:床足、床板、床面逐步剥落 六五:“贯鱼以宫人宠”:阴爻如鱼贯,得君主宠爱 上九:“硕果不食”:唯一阳爻如仅存硕果 金景芳:象征正气不绝,希望犹存 四、复卦(地雷复)的一阳来复 1. 与剥卦的转化 剥极必复:上九阳爻落到初位即成复卦 一阳初生:冬至之象,阳气复苏 2. 《彖传》的精微哲理 “复,其见天地之心乎”**:金景芳重点讲解 “天地之心”:天地化生万物的仁心 在阴气极盛时,看出阳气复生的天地本心 联系宋儒“仁者天地生物之心” 3. 爻辞的复归之路 初九:“不远复”:过失不久即回复正道 《系辞》“颜氏之子其殆庶几乎,有不善未尝不知,知之未尝复行” 六二:“休复”:美好的回复 六四:“中行独复”:与众人中独自回复正道 五、本课四卦的宇宙人生循环 社会秩序:噬嗑(法治)→ 贲(文教) 阴阳消长:剥(阴盛)→ 复(阳生) 金景芳总结:体现《周易》的“循环往复,生生不息”的宇宙观 与十二消息卦的关系:重点讲解剥(九月)、复(十一月)在阴阳消长周期中的位置

▶
临、观之道——领导与观察的智慧 一、临卦(地泽临)的领导艺术 1. 卦象的象征 上坤下兑:地临泽上,居高视下 “临”:监临、领导、面对 2. 四种领导方式(爻辞精析) 初九:“咸临,贞吉”:以感化领导(咸通感) 九二:“咸临,吉无不利”:以刚中之道感化 六三:“甘临,无攸利”:以甜言蜜语领导,必无利 六四:“至临,无咎”:亲临第一线 六五:“知临,大君之宜”:以智慧领导,君主典范 金景芳重点:与《中庸》“唯天下至圣为能聪明睿知,足以有临也”互证 上六:“敦临,吉无咎”:以敦厚之道领导 3. 《大象传》应用 “泽上有地,临。君子以教思无穷,容保民无疆” “教思无穷”:教育关怀永不止息 “容保民无疆”:包容保护百姓无边无际 金景芳:这是儒家德治思想的集中表达 二、观卦(风地观)的观察智慧 1. 卦象的双重观察 上巽下坤:风行地上,遍观万物 观:观察、展示、观念 2. 观察的四个层次 初六:“童观”:幼稚观察,小人无咎君子吝 六二:“窥观”:狭隘观察(女子利于贞) 六三:“观我生进退”:观察自我行为以调整进退 六四:“观国之光”:观察国家政教光辉 金景芳联系“观礼”制度:士人观察国家礼仪以决定去就 九五:“观我生,君子无咎”:君主自我观察 上九:“观其生,君子无咎”:观察民生 3. 《彖传》的宏大视野 “大观在上”:指九五爻居中得正 “下观而化”:下层观察上层而被感化 “观天之神道而四时不忒”:观察天道运行规律 金景芳重点:观卦体现《周易》的认识论——观察是行动的基础 三、临观二卦的领导学意义 内外之道:临卦重领导实践,观卦重观察认知 德治典范:临以教保民,观以神道设教 与《大学》“修身齐家治国平天下”的对应关系

▶
居安思危——豫卦的忧患意识与随、蛊的治乱之道 一、豫卦(雷地豫)的双重性 1. 卦象矛盾分析 上震下坤:雷出地奋,象征安乐、愉悦 但卦辞直言“利建侯行师”:暗含安乐中的危机 2. 《彖传》精讲 “刚应而志行”:九四阳爻为卦主,与初六相应 “顺以动”:下坤顺,上震动 “天地以顺动,故日月不过而四时不忒” 金景芳重点:真正的“豫”是顺应规律的和谐状态 3. 爻辞的警示梯度 初六:“鸣豫,凶”:稍有安乐就张扬,必凶 六三:“盱豫悔,迟有悔”:媚上求乐,必有悔恨 九四:“由豫,大有得”:作为安乐来源的阳爻,需“勿疑朋盍簪” 重点:领导者创造安乐时需团结众人 上六:“冥豫,成有渝”:沉溺安乐到极点,但提示“有渝”(可改变) 金景芳:体现《周易》永不绝望的哲学 二、随卦(泽雷随)的追随智慧 1. 卦象与卦名 上兑下震:泽中有雷,雷随泽动 “随”:随从、随和、随时 2. 金景芳卦变分析重点 随卦来自否卦:上九与初六互换(“刚来下柔”) 象征上位者主动下交,下层自然随从 对比“强随”与“悦随”的区别 3. 关键爻辞解析 初九:“官有渝,贞吉”:主变而不失正道 六二:“系小子,失丈夫”:选择困境,讲解“随”需有选择 九五:“孚于嘉,吉”:以诚信随善美,得吉 金景芳总结:“随”不是盲从,是“随时之义” 三、蛊卦(山风蛊)的整治之道 1. 卦象与问题意识 上艮下巽:山下有风,风被山阻而生腐败(蛊) 序卦传:“以喜随人者必有事,故受之以蛊” 2. 《彖传》精讲 “刚上而柔下”:上艮刚,下巽柔 “巽而止,蛊”:过于顺从(巽)而停滞(止)必生腐败 “终则有始”:整治腐败后又是新的开始 3. 爻辞的整治方略 初六:“干父之蛊”:整治父辈遗留问题 金景芳重点:继承中的改革,“意承考也”(继承精神而非具体做法) 九二:“干母之蛊”:方法需更柔和 上九:“不事王侯,高尚其事”: 重点讲解:整治完成后功成身退的智慧 对比道家隐逸思想 四、本课三卦的内在联系 忧患链条:豫(安乐)→ 随(盲从)→ 蛊(腐败) 治理智慧:豫时需思危,随时需择善,蛊时需整治 金景芳历史观体现:结合文景之治到汉武盛世的历史周期分析

▶
主题17:谦德之光——谦卦六爻皆吉的奥秘 一、谦卦(地山谦)的独特性 1. 卦象的深刻象征 上坤下艮:地在上,山在下——山本高耸却居于地下 金景芳指出:这是《周易》中唯一六爻皆吉的卦,深究其因 2. 《彖传》逐句精解 “天道下济而光明”:天之道向下施予而显光明 “地道卑而上行”:地之道卑下而向上运行 “天道亏盈而益谦”:自然规律是减损盈满、增益谦虚 “地道变盈而流谦”:大地的规律是改变盈满、流向低洼 “鬼神害盈而福谦”:鬼神也会损害盈满、赐福谦虚 “人道恶盈而好谦”:人的本性厌恶骄傲、喜好谦虚 金景芳总结:谦德符合天、地、人、鬼神的普遍法则 二、六爻全吉的层次分析 1. 初六爻:“谦谦君子” 处最下位而谦:君子之基 金景芳引《象传》“卑以自牧”:以谦卑态度自我修养 2. 六二爻:“鸣谦” 居中得正,谦德外显而有声名 分析“中心得也”:发自内心的真诚 3. 九三爻:“劳谦君子” 全卦主爻:唯一阳爻居下卦之顶,有功而谦 《系辞》特别赞誉:“劳而不伐,有功而不德” 金景芳联系周公“一沐三捉发,一饭三吐哺”的劳谦精神 4. 六四爻:“㧑谦” “㧑”(挥):发挥谦德,无所不利 分析近君之位更需谦德 5. 六五爻:“不富以其邻,利用侵伐” 重点讲解:谦德并非懦弱 当正义不张时,以谦德为号召进行征伐(如武王伐纣) 6. 上六爻:“鸣谦,利用行师” 谦德广闻,可用兵征不服 金景芳强调:谦的最终目的是“平天下”,必要时用武力 三、《大象传》的现实转化 “地中有山,谦。君子以裒多益寡,称物平施” 裒多益寡:取有余补不足——经济公平 称物平施:衡量事物公平施予——社会正义 从个人修养到社会制度的完整谦德体系 四、谦卦的哲学深度 儒家道德形上学在《易》中的集中体现 与老子“柔弱胜刚强”的区别:儒家之谦是阳刚中的柔德 为何六爻皆吉:谦德使人始终处于“未满”状态,永远有进步空间

▶